boj-1018-체스판 다시 칠하기
boj_1018_체스판 다시 칠하기
🙋♂️들어가며
이번 문제는 패턴을 활용한 구현이다
풀이
먼저 문제를 읽어보면 우리는 생각을 해볼 수 있다.
입력값에 범위가 8 <= N, M <= 50 이다
그렇다면 2가지 8*8 체스판의 패턴 활용을 통해 같지 않을때만 각 패턴이 일치하지 않는 횟수에 증가시켜 대소비교가 가능하지 않을까?
패턴은 다음과 같겠다
pattern_w (white 부터 시작)
| W | B | W | B | W | B | W | B |
| B | W | B | W | B | W | B | W |
| W | B | W | B | W | B | W | B |
| B | W | B | W | B | W | B | W |
| W | B | W | B | W | B | W | B |
| B | W | B | W | B | W | B | W |
| W | B | W | B | W | B | W | B |
| B | W | B | W | B | W | B | W |
pattern_b (Black 부터 시작)
| B | W | B | W | B | W | B | W |
| W | B | W | B | W | B | W | B |
| B | W | B | W | B | W | B | W |
| W | B | W | B | W | B | W | B |
| B | W | B | W | B | W | B | W |
| W | B | W | B | W | B | W | B |
| B | W | B | W | B | W | B | W |
| W | B | W | B | W | B | W | B |
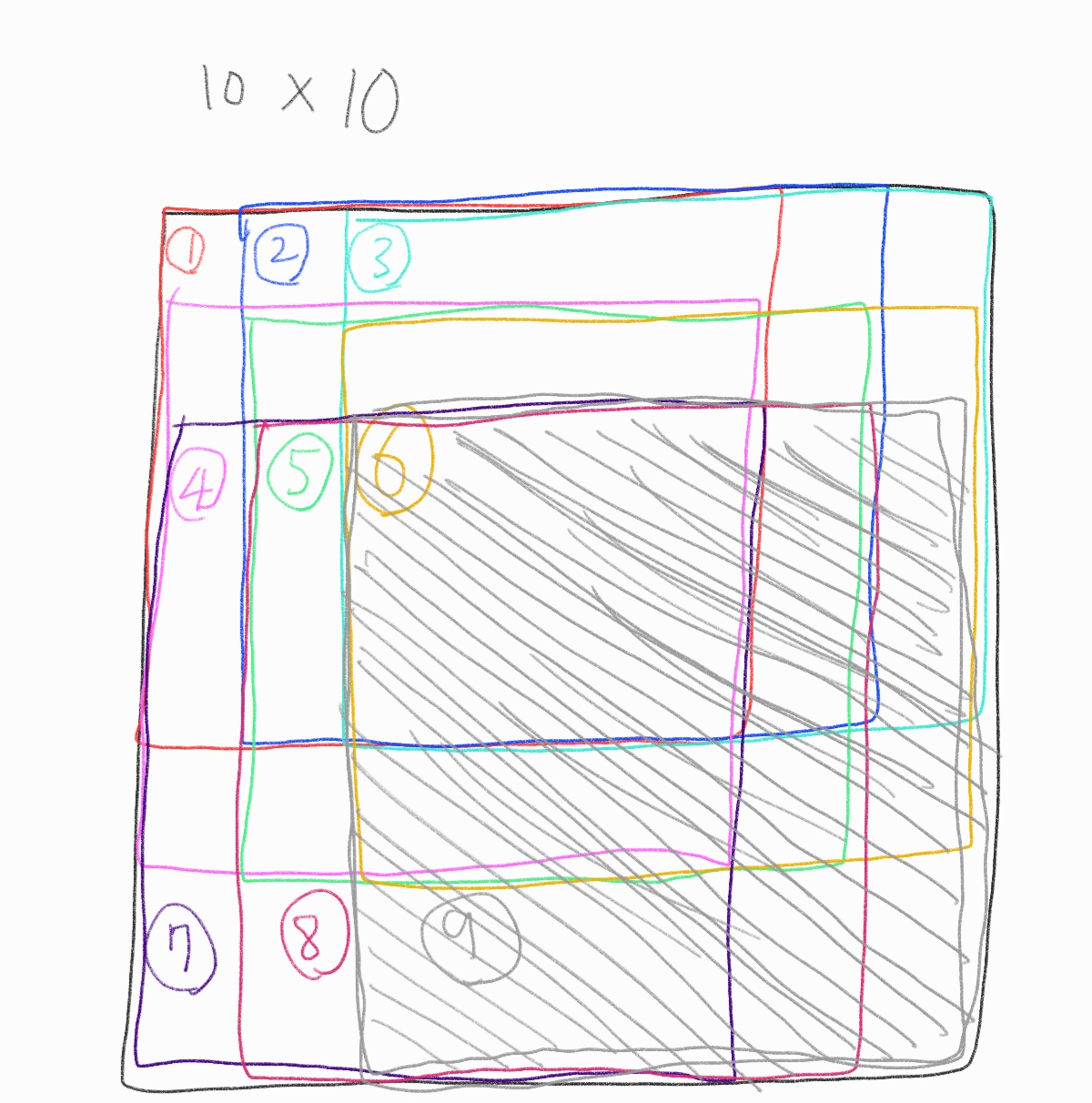
만약 N, M = 10 으로,
10*10 행렬인 경우, 2가지 패턴들이 아래처럼 각각 9회씩 탐색을 하겠다
그렇다면 코드로 보자
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
// 2가지 패턴을 만들어 비교한다
// 1. pattern_w (w로 먼저 시작)
// wb...
// bw...
// 2. pattern_b (b로 먼저 시작)
// bw...
// wb...
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.BufferedReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] NM = br.readLine().split(" ");
int N = Integer.parseInt(NM[0]);
int M = Integer.parseInt(NM[1]);
char[][] arr = new char[N][M];
for (int r = 0; r < N; r++) {
String cols = br.readLine();
for (int c = 0; c < M; c++) {
arr[r][c] = cols.charAt(c);
}
}
char[] p1 = {'W', 'B', 'W', 'B', 'W', 'B', 'W', 'B'};
char[] p2 = {'B', 'W', 'B', 'W', 'B', 'W', 'B', 'W'};
char[][] pattern_a = new char[8][8];
char[][] pattern_b = new char[8][8];
for (int r = 0; r < 8; r++) {
if (r % 2 == 0) {
for (int c = 0; c < 8; c++) {
pattern_a[r][c] = p1[c];
pattern_b[r][c] = p2[c];
}
}
if (r % 2 == 1) {
for (int c = 0; c < 8; c++) {
pattern_a[r][c] = p2[c];
pattern_b[r][c] = p1[c];
}
}
}
how_many_min_squares(N, M, arr, pattern_a, pattern_b);
}
static void how_many_min_squares(int N, int M, char[][] arr, char[][] pattern_a, char[][] pattern_b) {
int min_square = Integer.MAX_VALUE;
for (int r = 0; r < N-8 + 1; r++) {
for (int c = 0; c < M-8 + 1; c++) {
int cnt_a = 0;
int cnt_b = 0;
for (int b = r; b < r+8; b++) {
for (int a = c; a < c+8; a++) {
if (arr[b][a] != pattern_a[b-r][a-c]) cnt_a++;
if (arr[b][a] != pattern_b[b-r][a-c]) cnt_b++;
}
}
min_square = Math.min(min_square, Math.min(cnt_a, cnt_b));
}
}
System.out.println(min_square);
}
}
제출결과 -> 0.072초
This post is licensed under CC BY 4.0 by the author.