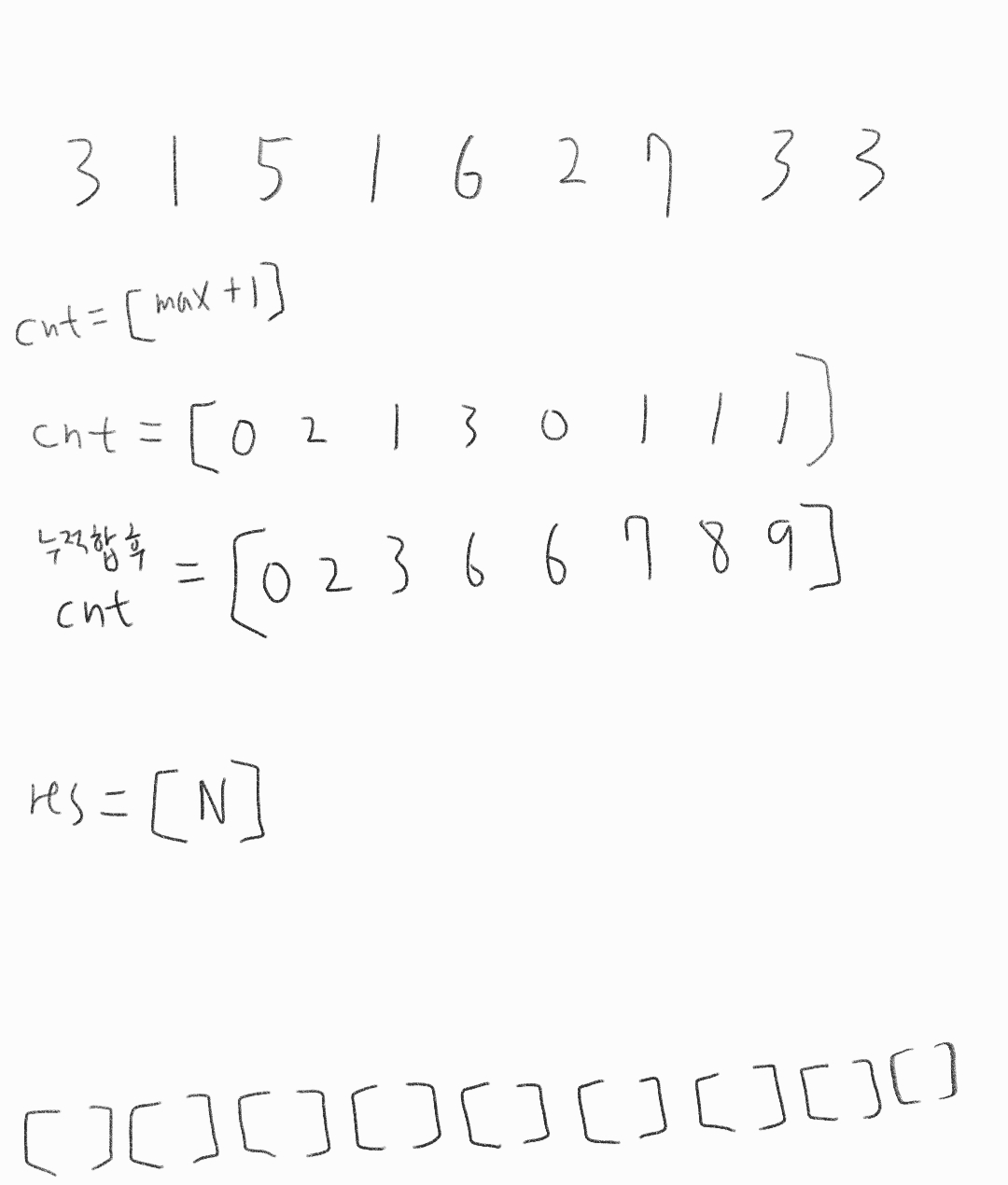counting sort

🙋‍♂️ 들어가며

이번에는 계수정렬 (카운팅 소트)를 배워보도록 하자

해당 알고리즘은 O(N+K)로 K는 값의 범위에 따라 바뀐다.

즉 최댓값이 작을 수록 좋다.

이제 구현을 해보자

🤔 시작

int[] arr = {3,1,5,1,6,2,7,3,3};

이런 배열이 있다고 가정하자

그 이후 cnt배열을 만들어 배열의 크기는 max_num + 1까지 만들고

arr의 숫자만큼 칸을 채워주자 그러면 다음과 같을 것이다

int[] cnt = {0, 2, 1, 3, 0, 1, 1, 1}

그다음 제일 중요한 누적합을 해줘야한다

그러면 다음과 같을 것이다

int[] cnt = {0, 2, 3, 6, 6, 7, 8, 9};

이제 계산을 하자 아래는 현재까지 진행된 상황이다.

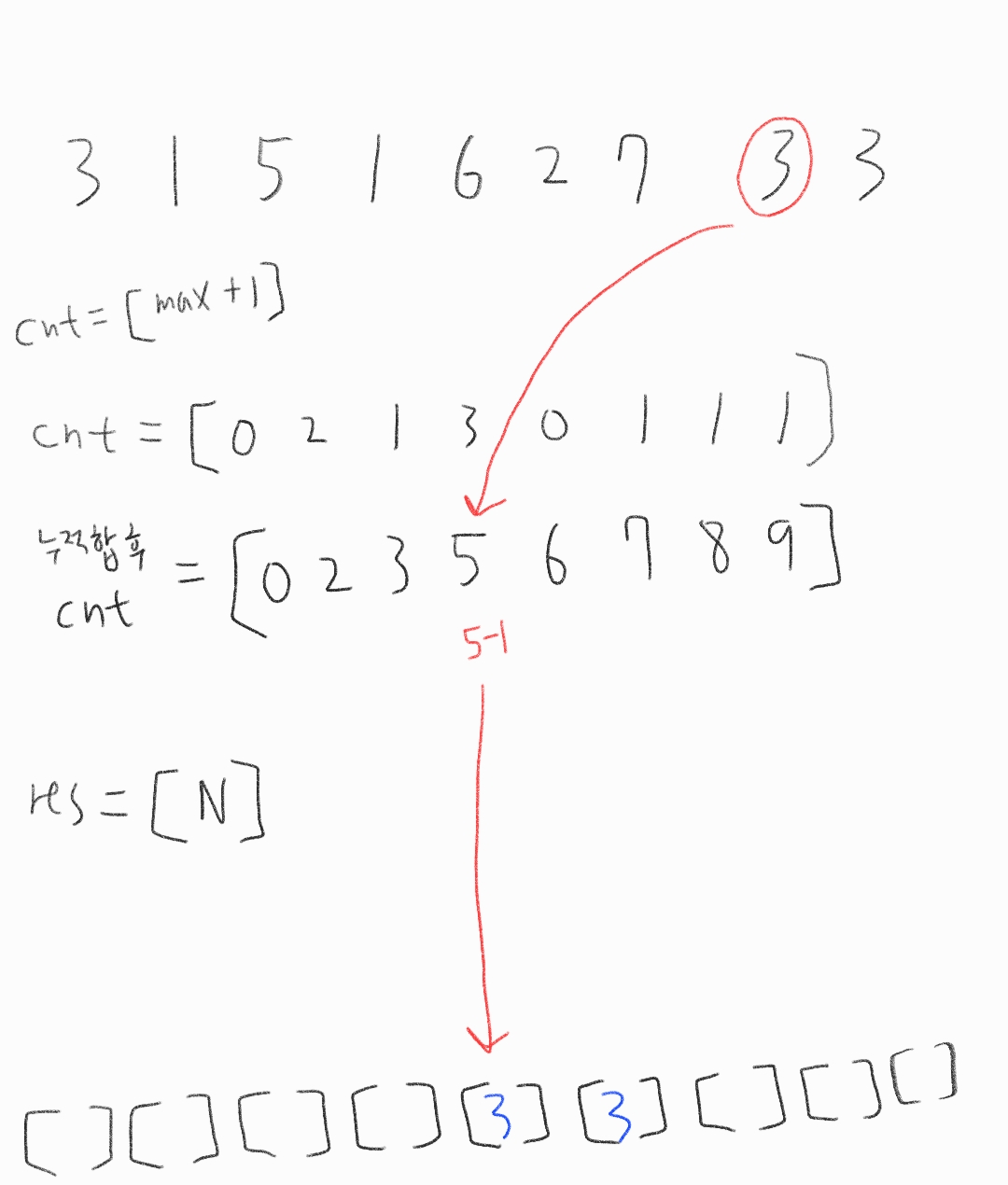
이제부터 거꾸로 계산을 하자

arr[i]를 cnt 배열의 idx로 찾아가고 그때의 값에서 -1 연산한 배열 자리로 그 값을 추가한다.

그리고 cnt 배열의 해당 idx 값을 1개 없앤다.

그 이유는 값이 여러개라면 앞으로 채워넣기 위함이다.

이제 맨 뒤원소를 봤으니 다음은 맨뒤에서 2번째를 탐색할 차례다

이어서 똑같이 진행되겠다.

다음

다음

다음

나머지도 똑같은 방식으로 res 배열이 채워지겠다

✅ 정답

int[] arr = {3,1,5,1,6,7,2,3,3};
int N = arr.length;

// 1. 최댓값 구하기
int max = 0;
for (int i = 0; i < N; i++) {
    if (arr[i] > max) max = i;
}

// 2. 카운팅 배열
int[] cnt = new int[max + 1];

// 2-1. 카운팅 배열 초기 추가
for (int i = 0; i < N; i++) {
    cnt[ arr[i] ]++;
}


// 2-2. 카운팅 배열 누적합 적용
for (int i = 1; i < cnt.length; i++) {
    cnt[i] += cnt[i-1];
}


// 3. 오름차순 정렬
int[] res = new int[N];
for (int i = N-1; i >= 0; i--) {
    int cur_val = arr[i];
    res[ cnt[ arr[i] ] - 1 ] = cur_val;
    cnt[ arr[i] ]--;
}

결과

res = {1, 1, 2, 3, 3, 3, 5, 6, 7};