미분방정식을 이용한 오일러 공식 유도
🙅♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다
1
2
3
4
<목차>
1. 들어가며
2. Euler's formula by differential equation
1. 들어가며
이번시간에는 오일러의 공식을 미분하여 증명할 것입니다.
오일러의 공식을 알게되면 시계열의 주기적인 현상이나 파동현상을 분석하는데 유용합니다
사전에 알면 좋은 것은 극좌표계(Polar Coordinates), 직교좌표계(Cartesian Coordinates)의 개념입니다.
알면 좋은 것 ʕ ·ᴥ·ʔ
2. Euler’s formula by differential equation
임의의 복소수 \(x+iy\)가 있을 때, \(x\)와 \(y\)를 실수라고 하자.
이 값은 극좌표계를 이용해 표현하면 다음과 같이 표현할 수 있다.
원점에서 \(x\), \(y\)까지의 거리가 \(r\)이고 \(x\)축과 이루는 각도가\(\theta\)라고 했을 때,
\(x+iy = rcos\theta+irsin\theta\)이다
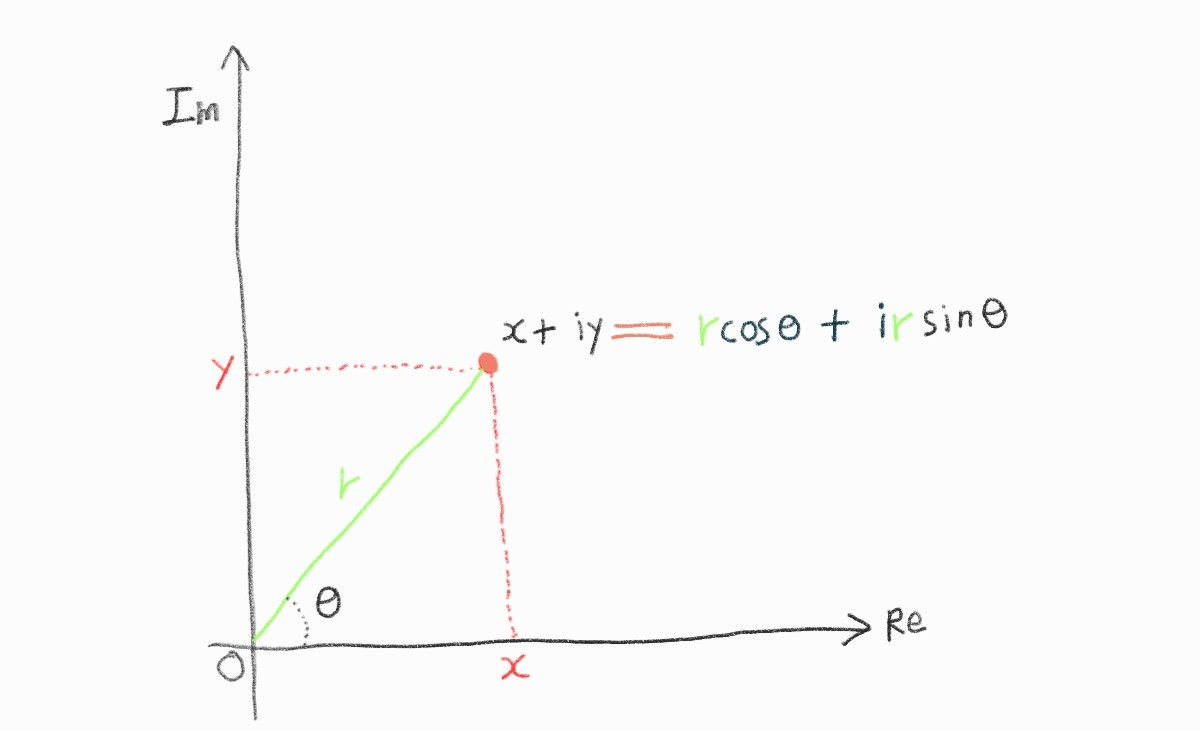
여기서 \(x\)와 \(y\)가 만나는 점을 \(x+iy\)로 나타내고 이를 직교좌표계에서 극좌표계로 변환해보면 아래와 같다.
\(x=cos \theta\)와 \(y=sin \theta\)를 이용하여 복소평면좌표 2차원 그래프에 있는 점인
\(x+iy\)를 나타내면 이는 \(r cos \theta + ir sin \theta\)가 된다
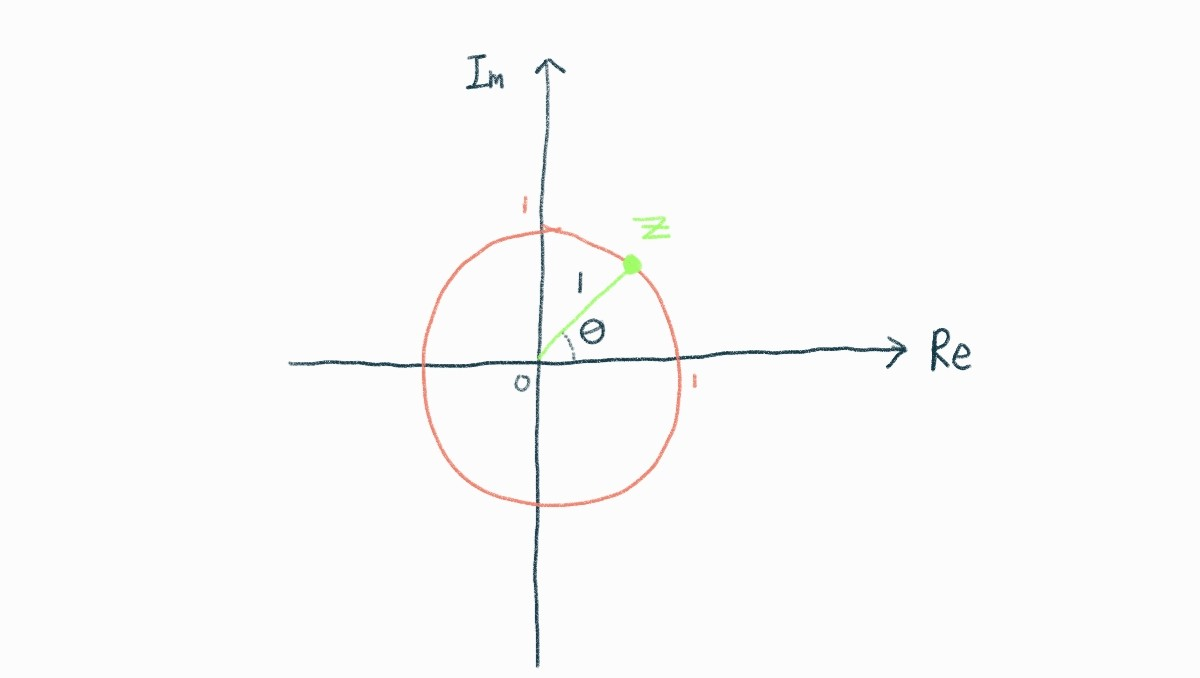
🧩증명
r=1 일때, 임의의 복소수 $z$가 있다고 하자
\(z = cos\theta + isin\theta\)
 양변을 \(\theta\)에 대해 미분하자
양변을 \(\theta\)에 대해 미분하자
\(\frac{dz}{d\theta} = -sin\theta + icos\theta\)
여기서 양변에 \(-i\)를 곱하자
\((-i)\frac{dz}{d\theta} = (-i)(-1)sin\theta + (-i)(i)cos\theta \\ = cos\theta + isin\theta\)
\(\therefore\) 어? \((-i)\frac{dz}{d\theta} = z\)네
여기서 한변을 \(z\), 다른 한변을 \(\theta\)에 대해 모아보면 아래와 같다
\(\frac{dz}{z} = \frac{1}{-i}d\theta\)
참! \(\frac{1 \cdot i}{-i \cdot i}=i\)니까, \(\frac{dz}{z}=id\theta\)
😎양변에 부정적분
(참고!: $log_ex$=\(lnx\))
그리고 잘 생각하자 우리가 적분하는 것은 complex number(복소수)다!
\(\int \frac{dz}{z} = \int id\theta \\ \rightarrow ln|z| = i\theta + C\)
참고! \(e^{ln|z|} = z\)
이게 무슨말이냐면 e와 ln이 곱해 \(|z|\)만 남는데 이는 \(z\)랑 같다
이걸 참고해 이제 적분했던 결과에서 이어서 해보면
\(z = e^{i\theta+c} = e^{i\theta}\cdot e^c = A_0 e^{i \theta}\)
$e^c$가 상수라서 \(A_0\)으로 바꿔주었다.
아까 위에 계산하고 남아있던 \(cos \theta + isin \theta\)를 합쳐주자
\(A_0 e^{i \theta} = cos \theta + i sin \theta \\ \therefore \theta = 0, \quad A_0 = 1 \\ \therefore e^{i \theta} = cos \theta + i sin \theta\) cos0일때 1, sin0 = 0, \(A_0\) = 1이 되니 자연스럽게 이 미분공식이 성립한다
만약 여기서 또 미분을 한다면?
\(\frac{d}{d \theta}(e^{i \theta}) = -sin \theta + i cos \theta = i(cos \theta + i sin \theta)\)
$ \color{pink}{\Rightarrow} $ \(i \cdot e^{i \theta} = i(cos \theta + i sin \theta)\)
여기서 \(-i\)를 양변에 곱해준다면 미분 1번 했을 때의 식이랑 같아진다
\(\therefore e^{i \theta} = cos \theta + i sin \theta\)