covariance matrix

🙅‍♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다

3명의 피실험자가 있다고 가정하자
피실험자1은 사과나 바나나를 먹으면 둘다 만족도1을 얻는다.
피실험자2는 사과를 먹으면 만족도3을 얻고 바나나에서는 얻지 못한다.
피실험자3은 사과랑 바나나를 먹을때 각각 불만족도 -1을 얻는다
(아무튼 과일을 정말 싫어한다는 뜻이다)

대상	사과	바나나
피실험자1	1	1
피실험자2	3	0
피실험자3	-1	-1

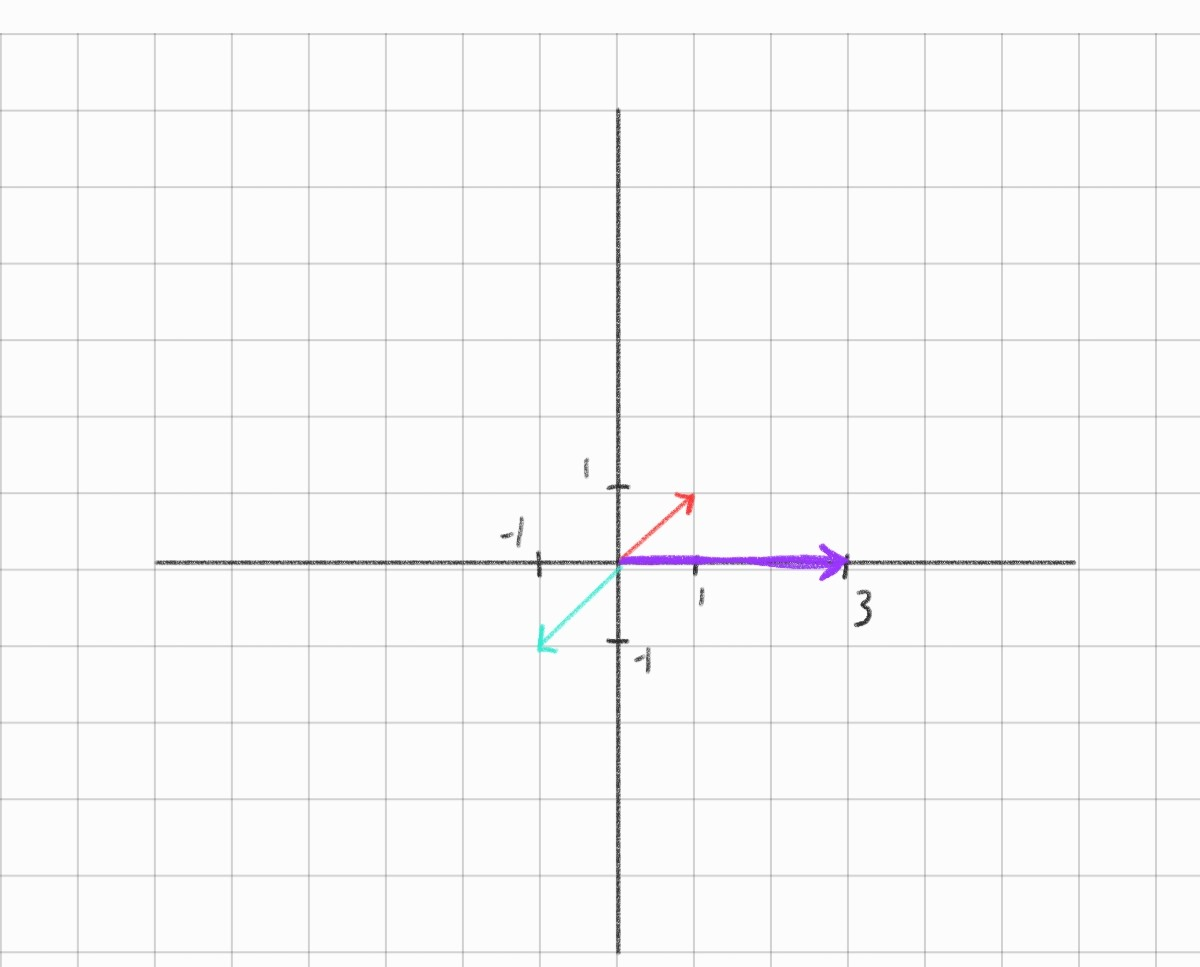
아래는 \(R^2\) 좌표에서 피실험자 3명을 각 벡터로 나타낸 것이다

변수는 x,y가 각각 사과, 바나나로 2개다
그래서 2x2 행렬이 되겠다
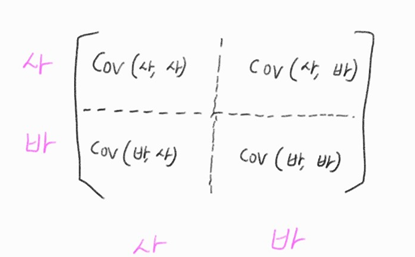
\(\begin{bmatrix} cov(x,x) & cos(x,y) \\cov(y,x) & cos(y,y) \end{bmatrix}\)

여기서 cov(사, 사)는 사과와 사과끼리의 공분산을 나타낸 것인데 이는 var(사)로 바꿀 수도 있다
마찬가지로 cov(바, 바) $\Rightarrow$ var(바)
이제 covariance matrix를 채우기 위해 사과와 바나나의 평균 계산하자
\(사과m \Rightarrow \frac{1+3-1}{3} \rightarrow 1\)
\(바나나m \Rightarrow \frac{1+0-1}{3} \rightarrow 0\)

covariance matrix process

\(Cov(A,B)\\=E(AB)-E(A)E(B)\)

여기서 E(AB)는 사과x바나나니까 각각 곱해 더하면 1, 0, 1 나온다
근데 3개니까 \(\frac{1+0+1}{3} \Rightarrow \frac{2}{3}\)
자 근데 가만보니 E(B)는 \(\frac{1}{3}+\frac{0}{3}-\frac{1}{3}=0\) 이 되기에 E(A)E(B)는 의미가 없어지므로 E(AB)만 구하면 되겠다

자 그럼 이번엔 cov(사, 사)를 구해보자
\(Cov(A,A)\\=E(A^2)-E(A)\)
\(E(A^2) \Rightarrow \frac{1^2+3^2+(-1)^2}{3} = \frac{11}{3}\)
\(E(A) \Rightarrow \frac{1+3-1}{3} = 1\)
\(\therefore \frac{11}{3}-1 = \frac{8}{3}\)

마지막으로 cov(바, 바)를 구하자
\(Cov(B,B)\\=E(B^2)-E(B)\)

아까 E(B)=0 이었으니 이건 제끼자
\(E(B^2) \Rightarrow \frac{1^2+0^2+(-1)^2}{3} = \frac{2}{3}\)
\(\therefore \frac{2}{3}-0 = \frac{2}{3}\)

$\color{red}{\therefore}$covariance matrix

\(\begin{bmatrix} \frac{8}{3} & \frac{2}{3} \\ \frac{2}{3} & \frac{2}{3} \end{bmatrix}\)

참고

[ritvikmath]    covariance matrix