Infinite Series & Definite Integral

🙅‍♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다

<목차>

1. 들어가며
2. 정적분
3. 무한급수와 정적분의 관계

1. 들어가며

무한급수와 정적분은 뗄레야 뗄 수 없는 관계를 갖고 있다 무슨 말이냐면
무한급수를 정적분으로 바꾸어 계산할 수 있고 정적분을 무한급수로 바꾸어 계산할 수 있다.

참!🤔 정적분을 언제 쓰지?
구간 [a, b]가 연속인 어떤 함수 f(x)가 있고
그 구간 사이에 가로의 길이가 같은 n개의 직각사각형의 넓이의 합의 극한값을 구할 때

🔒PreRequisites

1. limit
   
2. sequence
   

*참고
부정적분은 무조건 상수를 붙여 적분해야함
$\int x= x^2+C$

2. 정적분

개념을 정의하기 전에 정적분은 쉽게 말해 수열의 합의 극한 값으로
n개의 직사각형들의 각 넓이의 합의 극한값이라고 보면 된다
잠깐 아래 그림을 보자

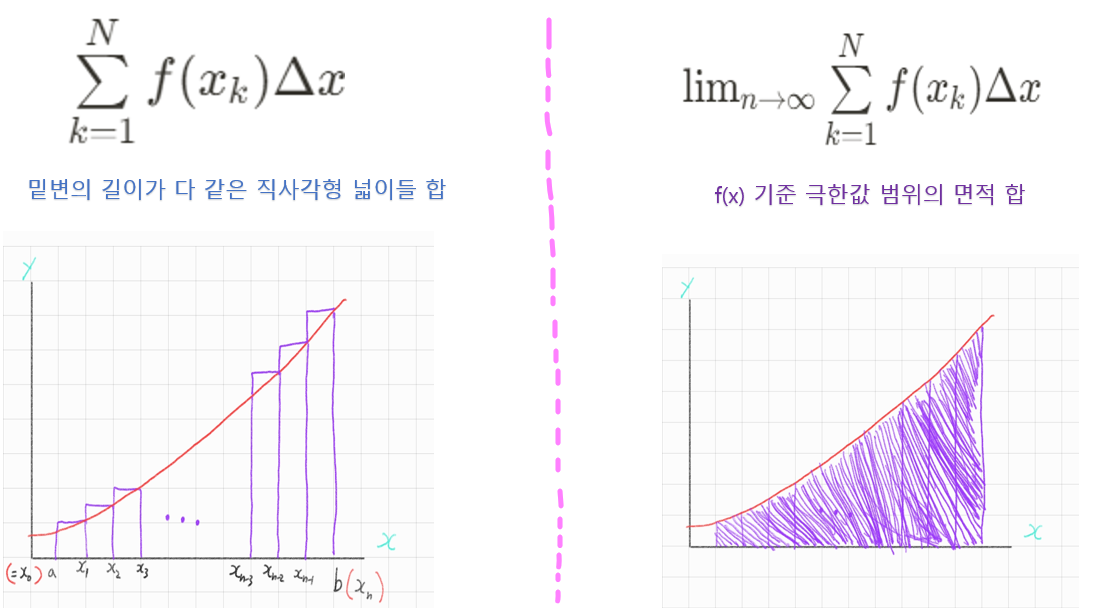
이 그림을 대충 한번 한번 훑어 보니 2개의 차이는 극한값 유무다
그냥 “이런게 있구나”정도로 생각하고 넘어가면 될 것 같다.
밑에서 제대로 설명하겠다

개념:

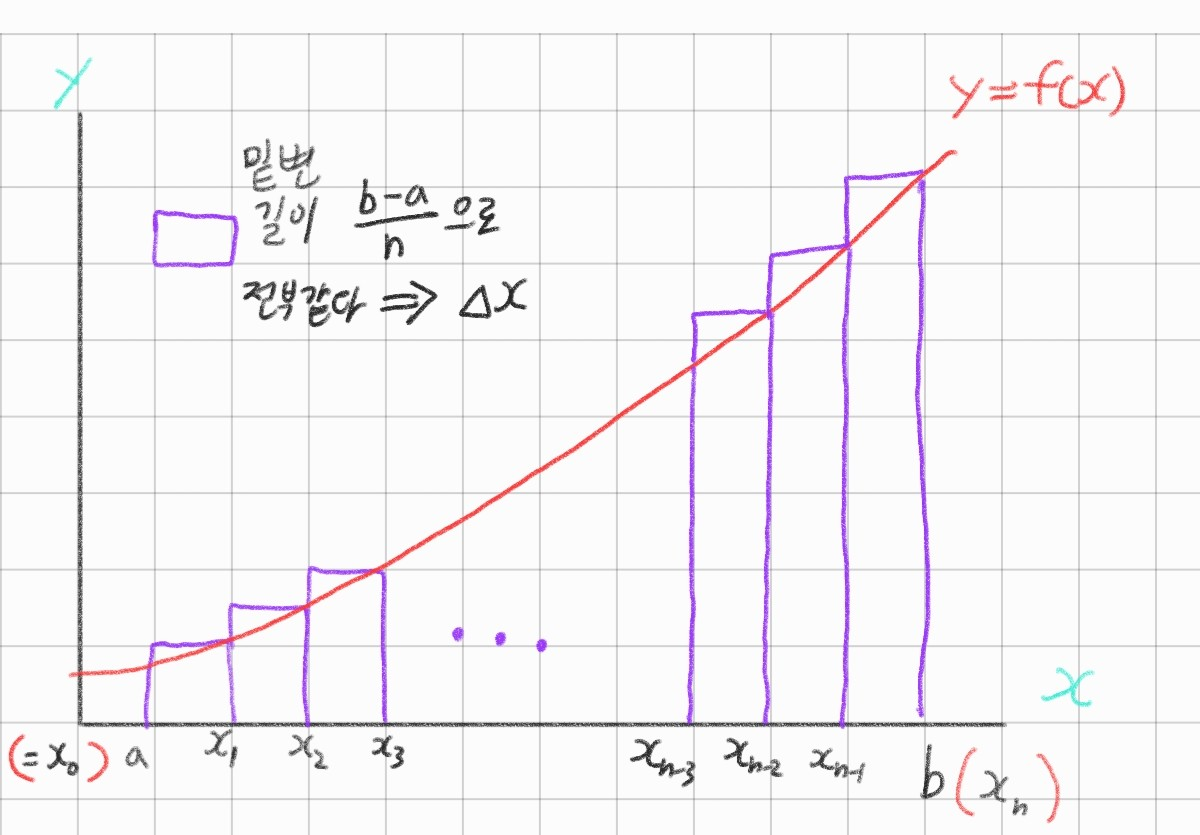
함수 \(f(x)\)가 구간 [a, b]에서 연속일 때, 그 구간을 n등분하여 양쪽 끝과 각 분점의 \(x\)좌표를 \(x_0(=a), x_1, \cdot\cdot\cdot, x_{n-1}, x_n(=b)\)라 하고 \(\frac{b-a}{n} = \Delta x\)라 할 때
\(\lim_{n\to\infty}\sum\limits_{k=1}^Nf(x_k)\Delta x\) 의 값을 함수 \(f(x)\)의 a에서 b까지의 정적분이라하고
그 값을 \(\int^b_a f(x)dx\)로 나타낸다

\(\color{red}{\therefore}\)   즉 \(\lim_{n \to \infty} \sum\limits_{k=1}^N f(x_k) \Delta x\) \(\color{red}{=}\) \(\int^b_a f(x)dx\) 이다

쉬운 이해를 위해 아래 그림을 보자
(아래 그림은 \(\lim_{n \to \infty}\)를 뺀 n개의 모든 보라 직사각형의 넓이를 \(\sum\limits\) 한 값이다)

여기서 보라색 벽돌 1개 칸의 길이는 \(\frac{b-a}{n}\)이다
왜냐하면 전체 길이는 b-a고 n등분 했으니까
아무튼 이것을 \(\Delta x\)로 두었다 (즉 보라색 벽돌 각각의 밑변의 길이가 됨)

자세한 설명

직사각형 넓이의 합

\(\color{red}{\frac{b-a}{n}}\) \(\left[ f\left(a+ \frac{b-a}{n}\right) + f\left(a+ \frac{b-a}{n}2\right) + \cdots f\left(a+ \frac{b-a}{n}n\right) \right]\)
이 식은 \(\color{red}{가로}\)[1번 직사각형 높이 + 2번 직사각형 높이 + … + 마지막 직사각형 높이 ]이다
여기에 f(함숫값)을 그래프에 넣으면 높이가 자연스럽게 나올 것이다

이제 이를 짧게 표현한 것이 아래와 같다
\(\sum\limits_{k=1}^n \frac{b-a}{n} f \left(a+ \frac{b-a}{n}k \right)\)

직사각형 넓이합을 적분으로 변환

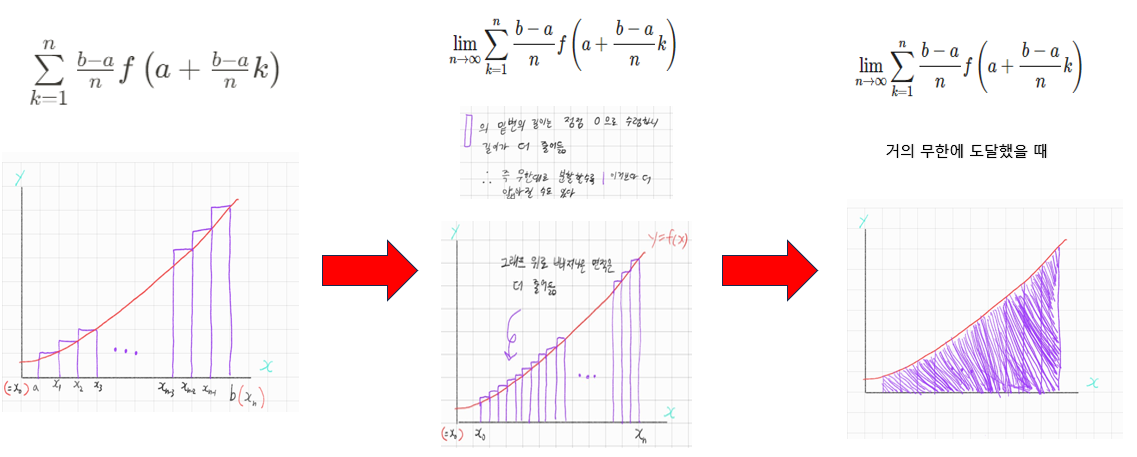
\(\lim_{n \to \infty} \sum\limits_{k=1}^n \frac{b-a}{n} f \left(a+ \frac{b-a}{n}k \right)\)
앞서 얘기했듯이 적분은 n개의 직사각형들의 각 넓이의 합의 극한값이니 $\lim_{n\to \infty}$ 표시를 하자
하게 되면 아래 그림의 과정을 거친다

우리가 그림을 보고 알 수 있는 것은 n이 무한으로 가까워 갈 수록
y=f(x)위의 삐져나온 면적들이 줄어들면서 결국 없어지는 것이다
그말은 즉슨 각각의 보라색 직사각형 밑변 길이도 머리카락처럼 얇아지며 결국 0이 된다는 말이다
(참 보라색 직사각형 각 밑변의 길이는 전부 n등분 한 것이라 똑같다 아까 위에서도 말했지만)

여기서 식을 좀 더 간단하게 나타내기 위해 아래 3가지들을 간소화 시키겠다
😗 \(\lim \sum_{n \to \infty}\) = \(\int\)

😀 \(a+ \frac{b-a}{n}k\) \(\color{red}{\Rightarrow}\) \(x\)

🫡 \(\frac{b-a}{n}\) \(\color{red}{\Rightarrow}\) \(dx\)

여기서 k가 1~n까지니 대입하면 범위는 a~b로 나오겠네

\(\therefore \int^b_a f(x)dx\)으로 부호가 있는 직사각형 넓이 합의 극한값이 된다
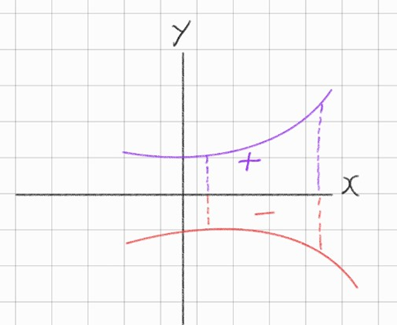
참 위의 그림에서는 면적이 양(+)의 부호인 넓이의 합의 극한값인데
사실 양(+) 음(-) 둘다 상관없다    아래 그림을 확인하자

3. 무한급수와 정적분의 관계

여기서는 평행이동과 축소 및 확대가 중요하다
이 글에서는 4가지 넓이 범위가 다 같은 식을 볼 것이고,
우선 아래의 무한급수 식을 기준으로 삼겠다
---------------기준식-----------------
\(\lim_{n \to \infty}\sum\limits_{k=1}^n f \left( a+ \frac{p}{n}k \right) \frac{p}{n}\)
-----------------------------------------

case 1) 기준식과 넓이가 같은 경우1(그냥 평범한 정적분)

이 식에서 정적분식으로 바꿔주기 위해 x와 dx를 아래와 같이 설정하자
\(\left( a+\frac{p}{n}k \color{red}{=} x \right)\)     \(\frac{p}{n} \color{red}{\Rightarrow} dx\)

여기서 k에 1이랑 n을 넣으면 $\infty$로 갈 때,
각각 a, a+p로 수렴하는데 이게 정적분의 범위다
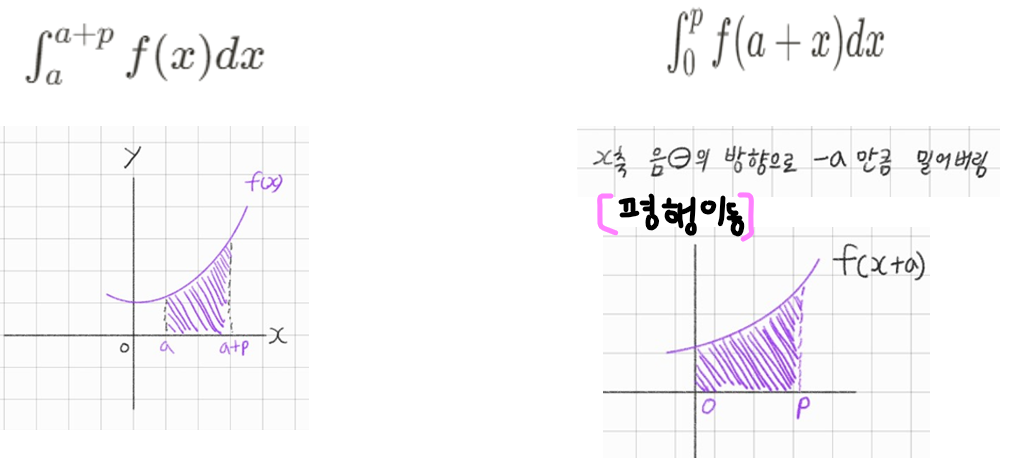
\(\color{red}{준식}\) = \(\int^{a+p}_a f(x)dx\)

case 2) case1과 넓이 합이 같은 경우2(case1에서 평행이동함)

\(\left( \frac{p}{n}k \color{red}{=} x \right)\)     \(\frac{p}{n} \color{red}{\Rightarrow} dx\)

마찬가지로 k에 1, n 각각 대입하면 \(\infty\)로 갈 때,
각각 0, p로 수렴한다
(맨 위의 기존식에 대입하는 것으로 헷갈리면 안된다! 여기서 해야한다)

자 그럼 a가 남았네?? = \(x \to x-a\)   (x방향으로 -a만큼 평행이동했다)
\(\color{red}{준식}\) = \(\int^{p}_0 f(a+x)dx\)

🖐️case1과 case2 비교

평행 이동한 차이가 잘 보이네ㅎ 그래서 면적은 둘다 같다

★추가

case1에서 x축으로 a만큼 이동한 것은 \(x \to x + a\) 한 것으로,
\(\color{red}{준식}\) = \(\int^{2a+p}_{2a} f(x-a)dx\)

case1에서 x축으로b만큼 이동한 것은 \(x \to x + b\) 한 것으로,
\(\color{red}{준식}\) = \(\int^{a+p+b}_{a+b} f(x-b)dx\)

\(\color{red}{\therefore}\) case1, 2 그리고 이 2개 추가 예시 합해서 4개는 전부 면적이 같다

case 3) \(\left( \frac{k}{n} \color{red}{=} x \right)\)로 설정할 때 (기준식 토대로)

\(\left( \frac{k}{n} \color{red}{=} x \right)\)     \(\frac{1}{n} \color{red}{\Rightarrow} dx\)
\(\color{red}{준식}\) = \(p\int^{1}_{0} f(a+px)dx\)

case 4) \(\left( \frac{k}{2n} \color{red}{=} x \right)\)로 설정할 때

맨 위의 무한급수 기준식은 아래와 같다
\(\lim_{n \to \infty}\sum\limits_{k=1}^n f \left( a+ \frac{p}{n}k \right) \frac{p}{n}\)

\(\left( \frac{k}{2n} \color{red}{=} x \right)\)     \(\frac{1}{2n} \color{red}{\Rightarrow} dx\)
이렇게 x와 dx를 설정하고 싶다면 무한급수 기준식을 아래와 같이 볼 수 있지 않을까
\(\lim_{n \to \infty}\sum\limits_{k=1}^n f \left( a+ 2p\frac{k}{2n} \right) \frac{1}{2n}2p\)

\(\color{red}{준식}\) = \(2p\int^{\frac{1}{2}}_{0} f(a+2px)dx\)

🖐️case3과 case4 비교

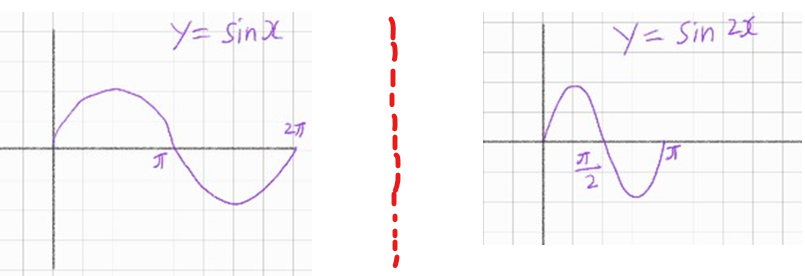
위 2개는 역시 같은 결과 값을 도출하는데 차이점이 있다면,   p와 2p 차이인데 축소 개념으로 보면 되겠다
즉 case4)의 함수가 case 3)의 함수에서 \(\frac{1}{2}\) 축소해서 구간도 \(\int^{\frac{1}{2}}_{0}\) 이렇게 절반으로 감소한 것이다
그래서 case4)의 함수에서 p에 2배를 해준 것이다
축소를 잘 모르겠으면 쉽게 이해하기 위해 아래 sinx와 sin2x 그래프를 보면 되겠다

참고

1. [큐스터디]     정적분과 무한급수
2. [수악중독]     부정적분