derivative

🙅‍♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다

<목차>
0. 알아야 할 것

1. 삼각함수의 도함수 
 1-1 (1)의 증명
 1-2 (2)의 증명
 1-3 (3)의 증명
 1-4 (4)의 증명
 1-5 (5)의 증명
 1-6 (6)의 증명
 1-7 위에 미분한 결과들을 적분하면?
 
2. 지수로그함수의 도함수
 2-1. (2) 증명
 2-2. (1) 증명
 2-3. (4) 증명
 2-4. (3) 증명

3. 속도와 가속도 
 
4. 미분 간단한 예시

5. 적분 간단한 예시

0. 알아야 할 것

※로그의 지수는 항상 +(양)부호다
※몫의 미분 (red)(매우 중요하다)
\(\left( \frac{f(x)}{g(x)} \right)' = \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{ \left\{ g(x) \right\}^2 }\)

ex) \(\left( \frac{1}{x} \right)' = \frac{0 \cdot x -1 \cdot 1}{x^2} = \frac{-1}{x^2}\)

1. 삼각함수의 도함수

(1) \((sinx)'= cosx\)
(2) \((cosx)' = -sinx\)
(3) \((tanx)' = sec^2 x\)
(4) \((cotx)'=-csc^2 x\)
(5) \((secx)' = secx \cdot tanx\)
(6) \((cscx)' = -cscx \cdot cotx\)
이거 쉽게 외우는 법 \(\color{red}{\Rightarrow}\) c로 시작하는데서 미분하는 것은 -부호가 붙네

1-1. (1)의 증명

\(f(x)=sinx\)

\((sinx)' = f'(x)=\lim_{h\to0} \frac{f(x+h)-f(x)}{h} = \lim_{h\to0} \frac{sin(x+h)-sin(x)}{h}\)
여기서 x+h \(\color{red}{\Rightarrow}\) A,     x \(\color{blue}{\Rightarrow}\) B라 설정하겠다
삼각함수 덧셈공식을 사용하자. 아래는 $sin(A-B)$에서 위치만 조금 바꾼 것이다 결과는 같다

🐼참고 \(sin(A)-sin(B)=2cos \left( \frac{A+B}{2} \right) sin \left( \frac{A-B}{2} \right)\)
그럼 위에서 정한A, B를 여기에 대입해보면 어떤 식이 또 산출되지?

위의 삼각함수 sin공식을 이용하여 \(\lim_{h\to0} \frac{sin(x+h)-sin(x)}{h}\)을 다시 전개하면 아래와 같다
\(\lim_{h\to0} \frac{2cos(x+\frac{h}{2}) \cdot sin(\frac{h}{2})}{h} = \frac{cos(x+\frac{h}{2}) \cdot sin(\frac{h}{2})}{\frac{h}{2}}\)

이렇게 변형시키면 우측 극한값인 sin쪽은 1로 수렴하고,
좌측 극한값인 cos쪽엔 \(cosx\) 로 수렴한다

1-2. (2)의 증명

\(f(x) = cosx\)

\((cosx)'=f'(x)=\lim_{h\to0} \frac{cos(x+h) - cos(x)}{h}\)
여기서 2x+h를 A+B,    h를 A-B로 보자
그리고 아래식 참고
\(cos(A)-cos(B) \\ =-2sin \left( \frac{A+B}{2} \right) sin \left( \frac{A-B}{2} \right)\)

이어서 위의 식에 대입하면 \(\lim_{h\to0} \frac{-2sin(x+\frac{h}{2}) \cdot sin(\frac{h}{2})}{h} = \lim_{h\to0} \frac{-sin(x+\frac{h}{2}) \cdot sin(\frac{h}{2})}{\frac{h}{2}}\)
이렇게 되면 전부 수렴하고 남는 것은 \(-(sinx \cdot 1) \cdot 1 \Rightarrow -sinx\)

1-3. (3)의 증명

\(f(x) = tan(x)\)

\(=\left( \frac{sin(x)}{cos(x)} \right)' = \frac{(sinx)\ \cdot cosx - sinx \cdot (cosx)'}{cos^2 x} = \frac{cos^2 x + sin^2 x}{cos^2 x} = \frac{1}{cos^2 x} \\ \therefore sec^2 x\)

1-4. (4)의 증명

\(f(x) = (cotx)'\)

자 cot이 뭐냐?   바로 \(\frac{1}{tanx}\)지 않느냐
\(\color{pink}{\Rightarrow}\) \(\frac{(-sinx) \cdot sinx - cosx \cdot cosx}{sin^2 x} = \frac{-1}{sin^2 x} = -csc^2 x\)

1-5. (5)의 증명

\(f(x)= (secx)'\)

\(=\left( \frac{1}{cos(x)} \right)' = \frac{0 \cdot cosx -1 \cdot(-sinx)}{cos^2 x} = \frac{1}{cosx} \cdot \frac{sinx}{cosx} = secx \cdot tanx\)
※삼각함수를 미분했을 때 각은 그대로 나온다!    ex) \(3x\)
ex-1) \((sec3x)' = 3 \cdot sec3x \cdot tan3 x\)
ex-2) \((tan6x)' =6 \cdot sec^2 6x\)

1-6. (6)의 증명

\(f(x)= (csc(x))'\)

바꿔쓰면 \(\left( \frac{1}{sin(x)} \right)'\) 이렇게 되는데 여기서 합성함수 미분공식 쓰자 \(\left( \frac{f(x)}{g(x)} \right)'\)
\(\Rightarrow\) \(\frac{0x \cdot sinx - 1 \cdot cosx}{sin^2x} = \frac{-1}{sinx} \cdot \frac{cosx}{sinx} = -cscx \cdot cotx\)

1-7. 위에 미분한 결과들을 적분하면?

(1) \(\int cosx dx = sinx + C\)
(2) \(\int sinx dx = -cosx + C\)
(3) \(\int sec^2xdx = tanx + C\)
(4) \(\int csc^2xdx = -cotx+C\)
(5) \(\int secx \cdot tanxdc = secx+C\)
(6) \(\int cscx \cdot cotxdx = -csc + C\)

2. 지수 $\cdot$ 로그함수의 도함수

(1) \(\left( e^x \right)' = e^x\)
(2) \(\left( a^x \right)' = a^x lna\)
(3) \(\left( lnx \right)' = \frac{1}{x}\)
(4) \(\left( log_ax \right)' = \frac{1}{x} \cdot \frac{1}{lna}\)
아래에 이해하기 쉽게 (2) → (1) → (4) → (3) 순으로 증명하겠다

2-1. (2) 증명

\(f'(x) = \left( a^x \right)' = \lim_{h\to0} \frac{f(x+h)-f(x)}{h} = lim_{h\to0} \frac{a^{x+h}-a^x}{h}\)

🎲참고
\(lim_{x\to0} \frac{a^{px}-1}{qx} = \frac{p}{q} \cdot lna\)
\(lim_{x\to0} \frac{a^{x}-1}{x} = lna\)

이걸 참고해서 이어서 전개하면
\(\lim_{h\to0} \frac{a^h-1}{h} \cdot a^x \Rightarrow a^x \cdot lna\)

\(\color{red}{ex)}\)
\(\left( 3^x \right)' = 3^x \cdot ln3\)
\(\left( 3^{2x} \right)' = \frac{2}{1} \cdot 3^{2x} \cdot ln3\)

2-2. (1) 증명

\(\left( e^{x} \right)' = e^x \cdot ln_e e = e^x\)

\(\color{red}{ex)}\)
\(\left( e^{3x} \right)' = 3e^{3x} \cdot ln_e e = 3e^{3x}\)

2-3. (4) 증명

\(f(x)=log_ax\) 라고 하자
\(\left( log_ax \right)' = f'(x) = lim_{h\to0} \frac{log_a(x+h) - log_a x}{h}\) 여기서 분모를 없애고 분자만 보자

🖐️잠깐 밑이 같은 로그를 빼면? \(\color{red}{\Rightarrow}\) \(log_a A- log_b B = log_a \frac{A}{B}\)
자 이를 활용하면 \(log_a\left(\frac{x+h}{x} \right)\)로 나타낼 수 있네?   자 그러면 아래에서는 x를 나누고 이어서 전개하겠다

\(= \lim_{h\to0} \frac{1}{h} \cdot log_a (1+\frac{h}{x})^{\frac{1}{h}}\) (red) \(=\) \(\lim_{h\to0} log_a (1+\frac{h}{x})^{\frac{x}{h} \cdot \frac{1}{x}}\)

어? 가만보니 \((1+\frac{h}{x})^{\frac{x}{h}} = e\) 네? \(log_a e^{\frac{1}{x}} = \frac{1}{x}log_a e = \frac{1}{x}\cdot\frac{1}{log_e a}\)
\(\color{purple}{\Rightarrow}\)   \(\frac{1}{x} \cdot \frac{1}{lna}\)

☆이것도 참고하자
ex-1) \(log_a s = \frac{1}{log_s a}\)
ex-2) \(\left(log_2 x \right)' = \frac{1}{x} \cdot \frac{1}{ln2}\)
ex-3) \(\left( log_2 3x \right)' = 3 \cdot \frac{1}{3x}\cdot \frac{1}{1n2}\)
ex-4) \(\left( log_a f(x) \right)' = \frac{f'(x)}{f(x)} \cdot \frac{1}{lna}\)
ex-5) \(\left( log_2 3^{2x} \right)' = \left( 2x \cdot log_2 3 \right)'\) \(\color{pink}{\Rightarrow}\) \(2 \cdot log_2 3\)

2-4. (3) 증명

\(f'\left( x \right) = \left( log_e x \right)' = \frac{1}{x} \cdot \frac{1}{ln_e e} = \frac{1}{x}\)

ex) \(ln(\Delta)' = \frac{\Delta'}{\Delta}\) \(\color{pink}{\Rightarrow}\) \(\{ ln(x^2+x+1) \}' = \frac{\{2x+1\} \cdot ln_e e}{\{x^2+x+1\} \cdot ln_e e} = \frac{2x+1}{x^2+x+1}\)

3. 속도와 가속도

메이플스토리의 와일드보어가 움직인다고 생각해보자
아래는 Cartesian coordinate system에서 \((x+k)x^2\) 을 나타낸 것이다

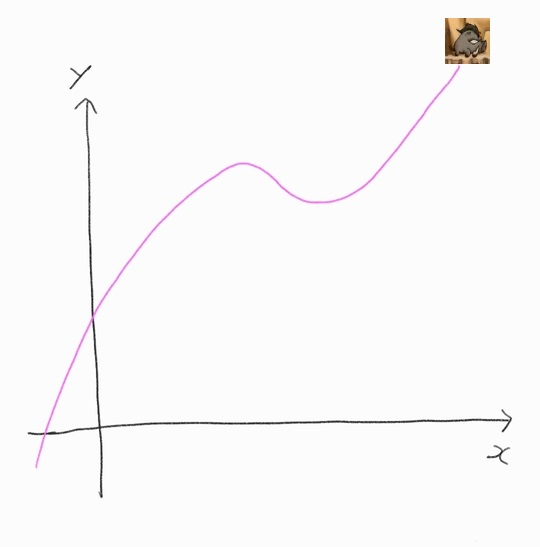
아래는 와일드 보어가 도달했던 구간들을 임의로 x축, y축을 이용해 나타낸 것이다

일반적으로 좌표평면 위를 움직이는 점 P의 t(시간)에서의 위치(x,y)는
t를 매개변수로 하는 두 함수 \(x=f(t)\),   \(y=g(t)\)로 나타낼 수 있다
참고로 \(`t(시간) >0`\) 당연한 것이다

다음은 와일드보어가 \(p_1(1, 6)\)에서 \(P_?(2, 17)\)까지 이동했을 때
t초 걸린 것에 대한 그래프를 나타낸 것이다.

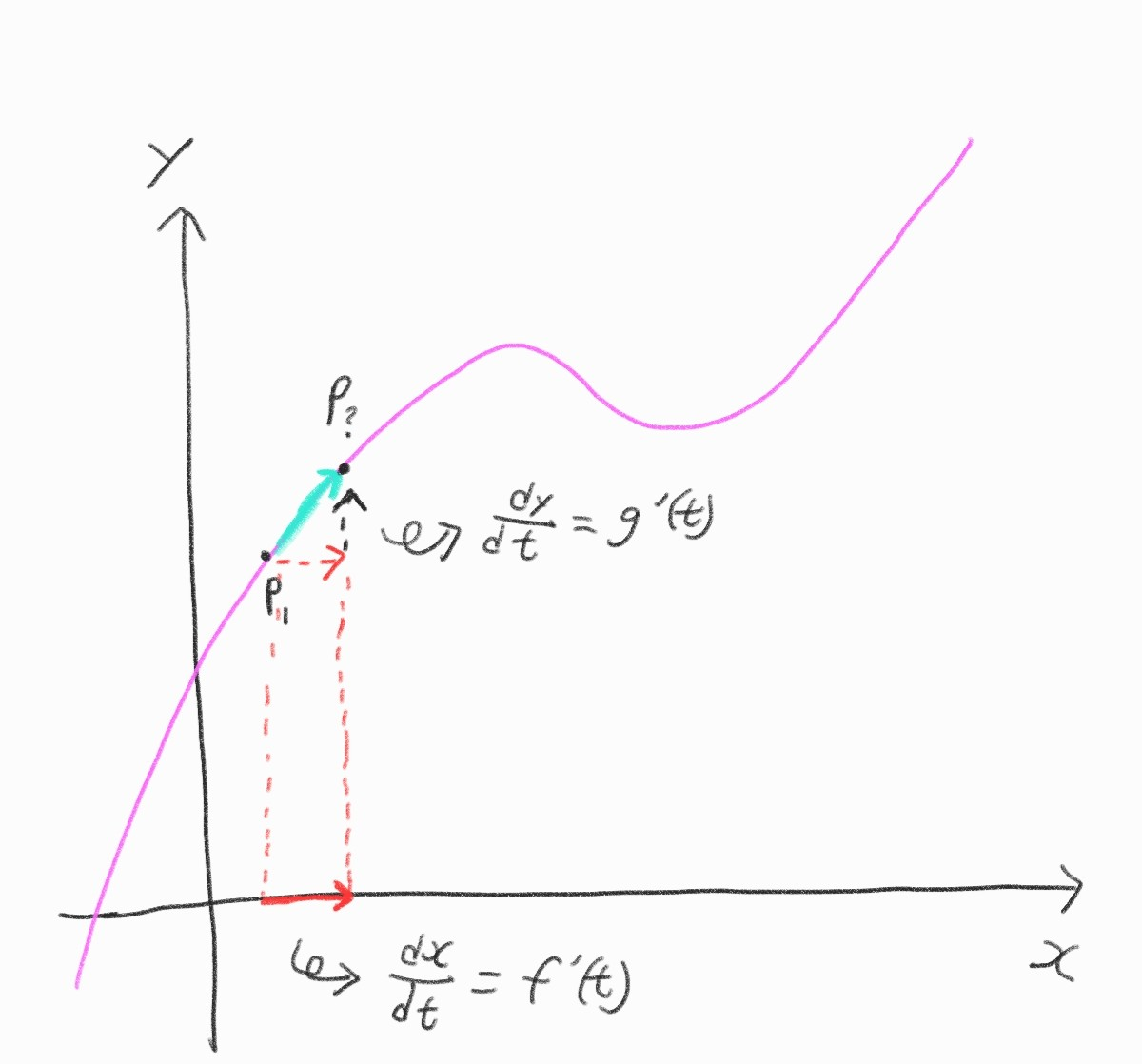
이때 점 P의 t(시간)에서의 속도와 속력, 가속도와 가속도의 크기는 다음과 같다
(1) 점 P에서 t(시간)에서의 속도와 속력
(2) 속도: ( \(f'(t), g'(t)\) )
(3) 속력: \(\sqrt{f'(t)^2 + g'(t)^2}\)
*거리:   \(t \cdot 속력\)
순간적인 x축과 y축의 변화율에 대해 \(\frac{dx}{dt} = f'(t)\)와 \(\frac{dy}{dt} = g'(t)\) 로 표현했다.

자 그러면 \(p_1 \rightarrow p_?\) 구간을 지나갈 때 3초 일때의 속력은 어떨지 계산해보자
피타고라스 정리를 연상하면 쉽다
우선 두점사이 거리 구하는 공식인 유클리드 거리 공식\(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\) 을 이용해서
\(\sqrt{122}\)가 나왔고 그 구간에서의 3초가 경과했을 때 속력은 \(\frac{\sqrt{122}}{3}\)이다

그렇다면 가속력은 어떻게??
(미분 2번이다)

(1) 가속도: \((f''(t), g''(t))\)
(2) 가속도의 크기: \(\sqrt{f''(t)^2 + g''(t)^2}\)

4. 미분 간단한 예시

함성함수의 미분: \((\clubsuit \cdot \Delta)'\) \(\color{pink}{\Rightarrow}\) \(\clubsuit' \cdot \Delta + \clubsuit \cdot \Delta'\)

ex-1) \(f(x) = e^x \cdot sin5x\)
\(f'(x) = e^x sin5x + e^x (5cos5x)\)

ex-2) \(f(x) = e^{-2x}cos3x\)
\(f'(x) = (-2 \cdot e^{-2x})cos3x + e^{-2x}(-3 \cdot sin3x) \\ = -e^{-2x}(2 \cdot cos3x + 3 \cdot sin3x)\)

5. 적분 간단한 예시

ex-1) \(\{ ln(x^2+1) \}' = \frac{2x}{x^2+1}\) 이것은 미분된 값이다
그럼 적분은?   \(\int \frac{2x}{x^2+1}dx = ln(x^2+1) + C\)

ex-2) \(\int tanx dx\)
\(= \int \frac{sinx}{cosx}dx = -\int \frac{-sinx}{cosx}dx \Rightarrow -ln |cosx| +C\)

ex-3) $\int e^{3x} dx = \frac{1}{3}e^{3x} + C$

ex-4) $\int cos3xdx = \frac{1}{3} sin3x + C$

참고

1. 큐스터디 전공수학  -  대학수학의 기초/ 미적분 강의 (3시간)
   
2. 제9장: 넓이와 기울기 사이 숨겨진 연결고리 미적분학의 본질
   
3. eo    미적분 기초부터
   
4. [2025 수능특강] 김민재의 미적분 - 28강 5-5. 속도와 가속도 & 도함수의 활용 Level Up (1)