DP

목차

1. dp(동적 계획법)의 특징

2. 팩토리얼을 통한 재귀함수 표현

3. 피보나치수열의 형태 및 한계

4. dp(동적계획법)을 활용한 한계 극복
1) Memoization (Top-Down, 하향식)
2) Tabulation (Bottom-up, 상향식)

1. dp(동적 계획법)의 특징

• 큰 문제를 작게 나누고, 같은 문제라면 한번만 풂
• 한번 계산한 문제는 다시 계산 안하는 알고리즘

2. 팩토리얼을 통한 재귀함수 표현

잠깐! 재귀함수란 무엇인가? —> 함수 안의 자신의 함수를 다시 호출

(자신의 로직을 반복하다 일정 조건이 만족되면 함수를 이탈하여 결과를 도출)

def factorial(x):
  if x > 1:
    return x * factorial(x-1)
  else:
    return x

for x in range(5+1):        # 0 부터 5까지 반복
  print(factorial(x))

# 결과
# 0
# 1
# 2
# 6
# 24
# 120

3. 피보나치수열의 형태 및 한계

• dp를 재귀 함수 중 하나인 피보나치수열에 적용 가능하다.
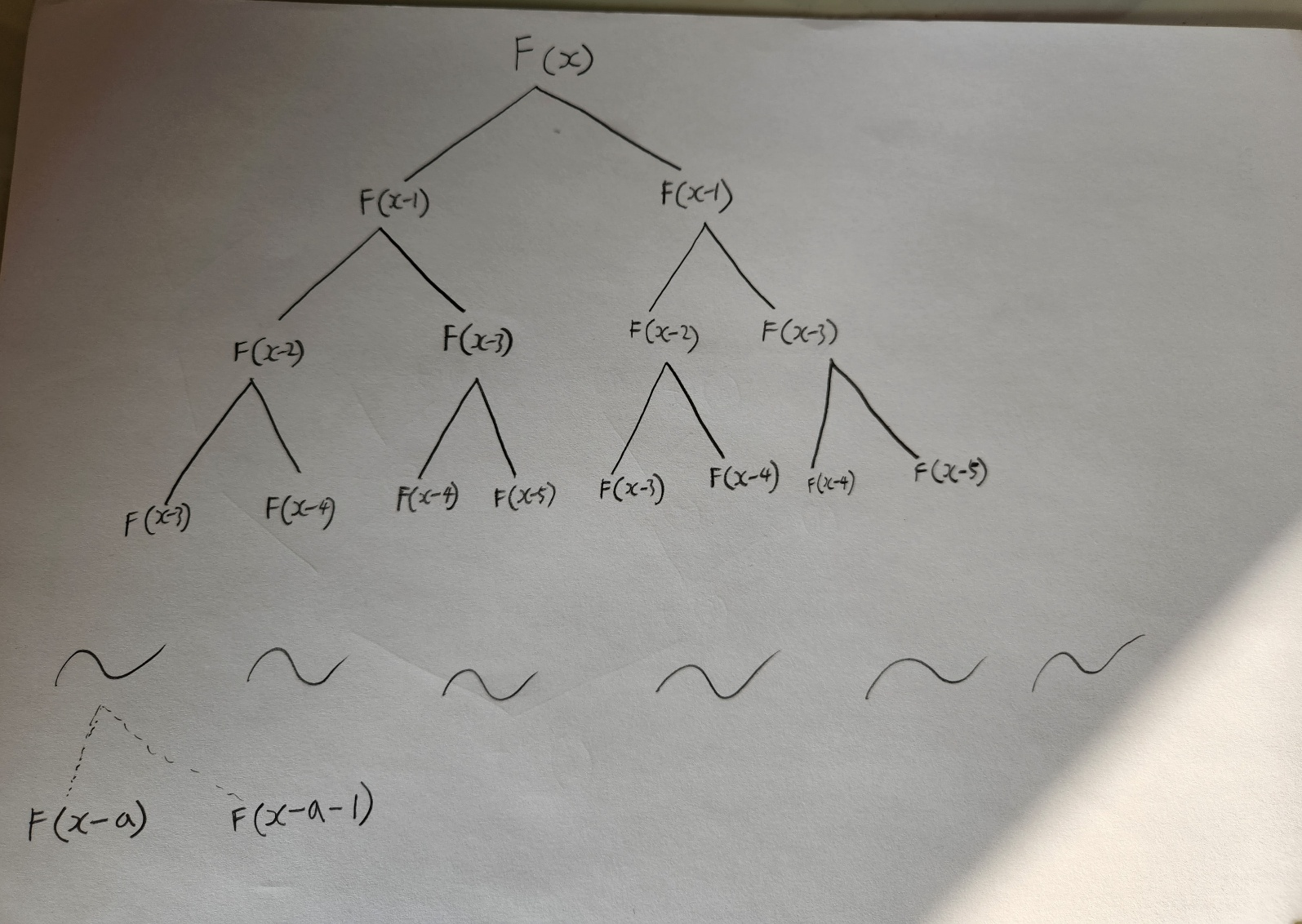
• 기본형태는 f(x) = f(x-1) + f(x-2)

def fibonacci(x):
  if x == 0:
    return 0
  elif x == 1 or x ==2:
    return 1
  else:
    return fibonacci(x-1) + fibonacci(x-2)

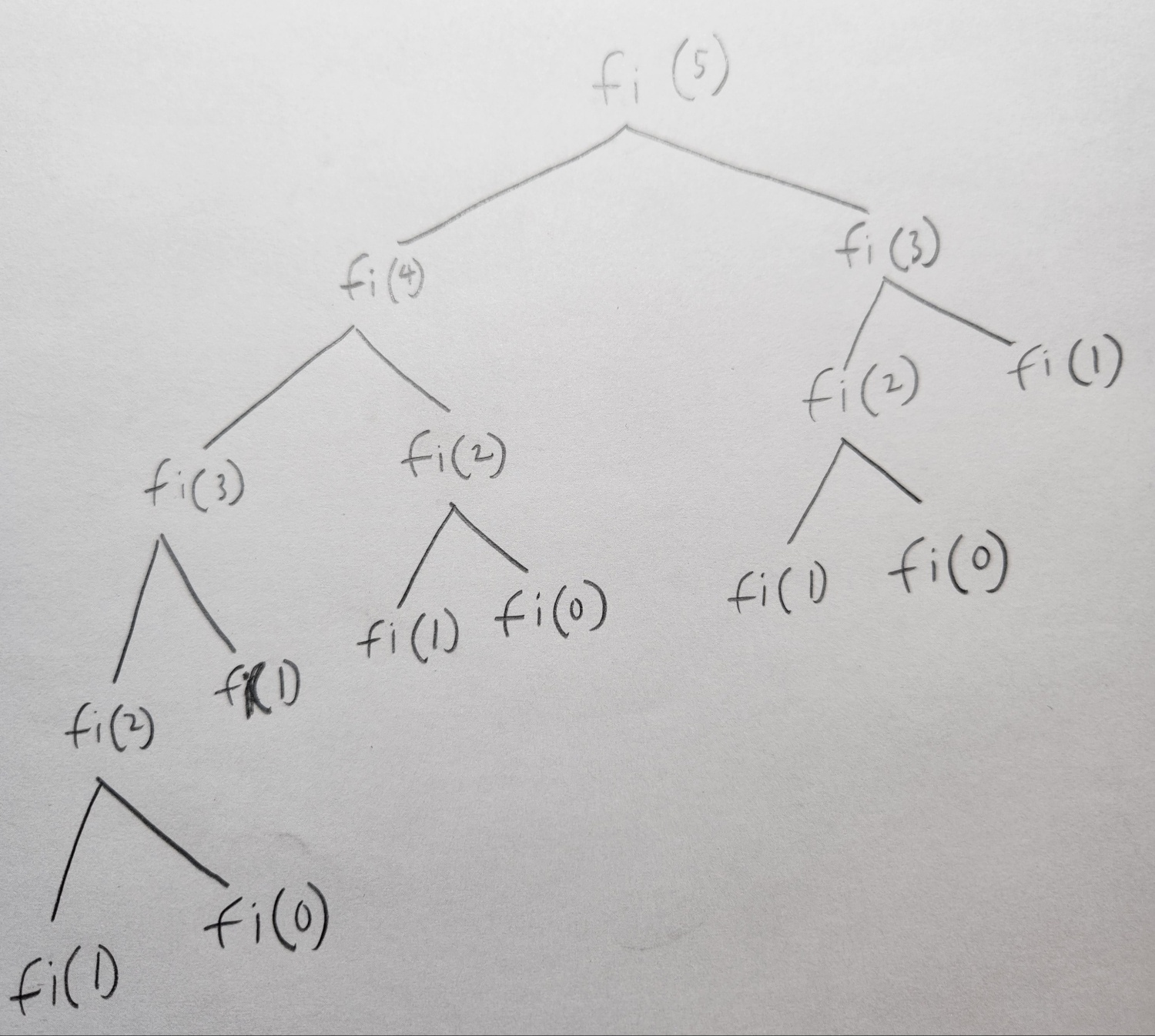
x = 5 일 때

★위의 도식화는 총 x=5 대입 후, 15회 계산한 것

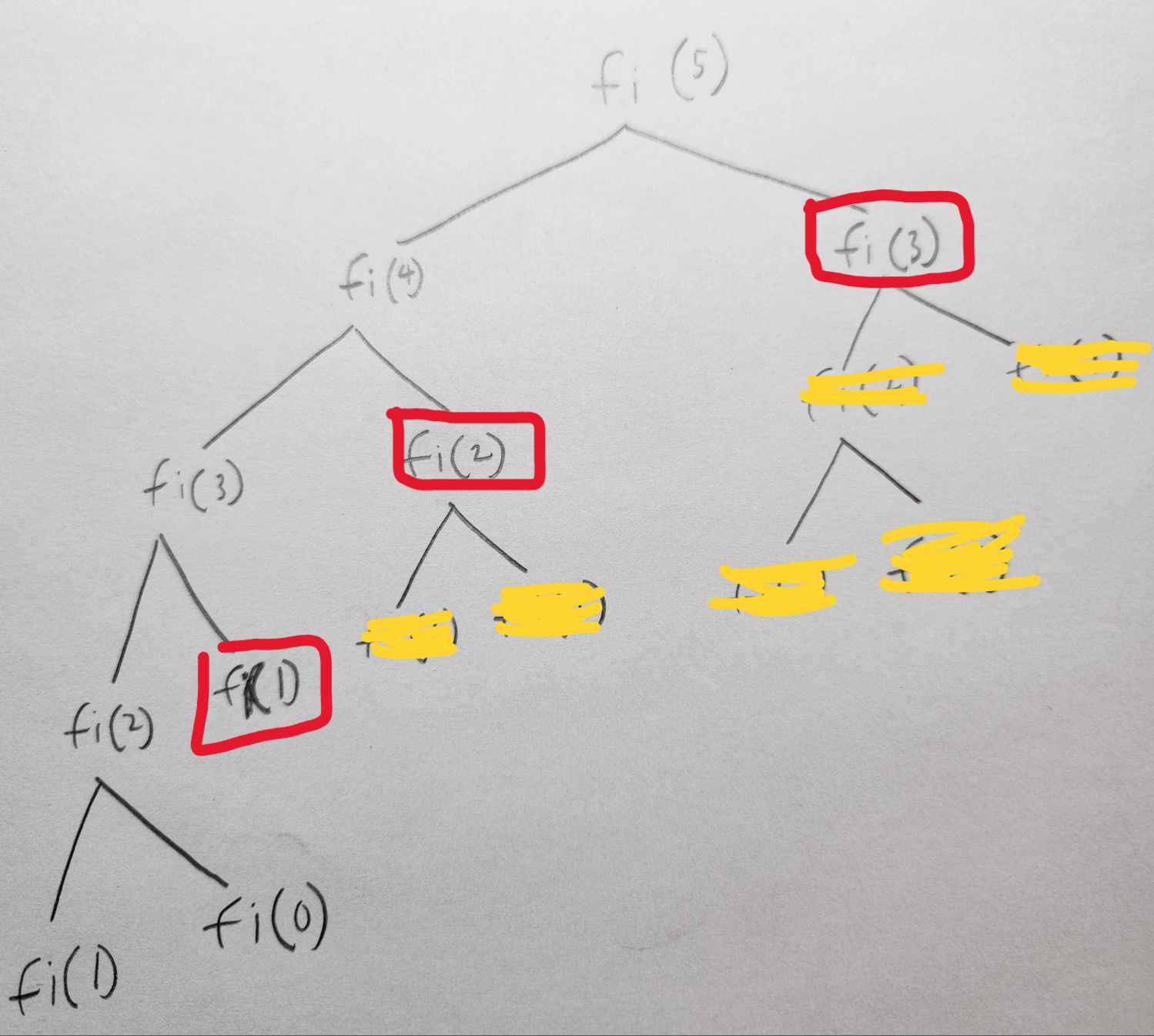
• 수기로 작성한 도식화를 보면 이미 한번 계산한 값도 계속 호출할 때마다 계산했다.
• 혹시 x가 크다면 기하급수적으로 계산과정이 길어진다.

4. dp(동적계획법)을 활용한 한계 극복

1). Memoization (Top-Down, 하향식)

하향식(Top-Down) 경우 하위 문제에 대하여 정답을 계산했는지 확인해가며 문제를 자연스럽게 풀어나가는 방법이다. 흔히 이를 Memoization이라고 부른다.

# DP, Memoization

dp_Memo=[0]*11
dp_Memo[0]=1
dp_Memo[1]=1

def fib_Memo(n):
    
    #한번도 계산한 적이 없는 경우
    
    if dp_Memo[n]==0: #dp list에 계산한적이 없는경우 0으로 저장되어 있음
        dp_Memo[n] = fib(n-1)+fib(n-2) #재귀로 계산하여 리스트에 값 추가
    
    # 새롭게 추가 값 혹은 저장된 값 반환
    
    return dp_Memo[n]

# 피보나치 수열 항 리스트 전체 출력
for i in range(11):
    fib_Memo(i)

print(dp_Memo)

fib_Memo(10)

"""
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]
output: 89
"""

2). Tabulation (Bottom-up, 상향식)

상향식(Bottom-Up)은 더 작은 하위 문제부터 살펴본 다음 작은 문제의 정답을 이용하여 큰 문제의 정답을 풀어나가는 방법이다.

# 풀이 1.
def fib_Tab1(n):
    
    dp_Tab=[0]*(n+1)
    dp_Tab[0],dp_Tab[1]= 1,1
    
    # 작은 값(소문제)부터 직접 계산하며 진행
    
    # 2항 ~ n항 까지 피보나치 수열항 계산 (0,1 항 = 1)
    for i in range(2,n+1):        
        dp_Tab[i]=dp_Tab[i-1]+dp_Tab[i-2]
    
    print(dp_Tab) # 피보나치 수열 항 리스트 전체 출력
    
    return dp_Tab[n]

fib_Tab(10)

"""
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]
output: 89
"""

# 풀이 2.

def fib_Tab2(n):
	p=[1,1]
	for i in range(2,n+1): # n번째 까지 피보나치 수열 나열
												 # 여기서 range 범위는 ***2 <= i < n***
		p.append(p[-1]+p[-2]) # 마지막 2 요소의 합을 리스트에 추가
		print(p)
	return(p[-1]) #피보나치 n번째 값 Return

fib_Tab2(10)
"""
output: 89
"""

참고

https://velog.io/@seulki971227/프로그래머스-Lv.3-정수-삼각형-Python

https://velog.io/@bonjaski0989/동적계획법Dynamic-Programming-정리글Python

https://data-marketing-bk.tistory.com/27