오일러공식을 이해하기 위한 쉬운 설명(회전변환)
🙅♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다
1
2
3
4
<목차>
1. 들어가며
2. 회전변환 증명
1. 들어가며
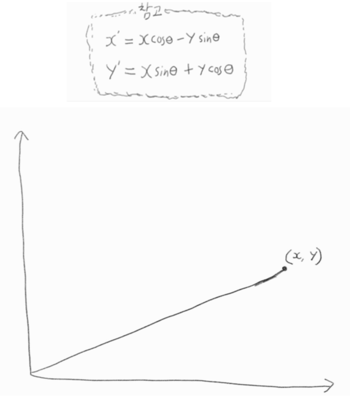
질문: 평면 위의 점 (x, y)를 \(\theta\)만큼 회전시키면 좌표가 어떻게 변할까?
2. 회전변환 증명
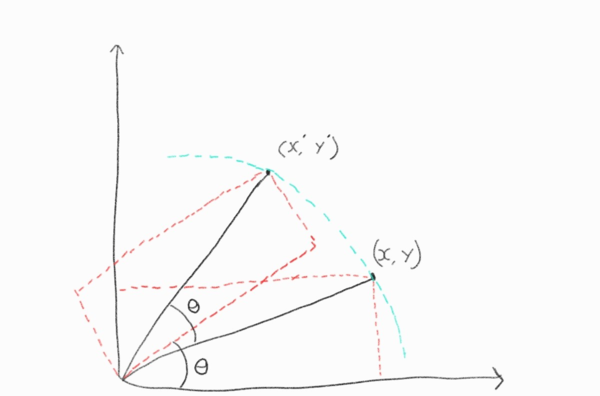
우선 (x’, y’)를 구하기 위해 아래의 직사각형을 생각해보자 그럼 그 직사각형 역시 \(\theta\)만큼 회전하여 놓이게 될 것이다.
아래는 결과 사진과 시뮬레이션.gif다.
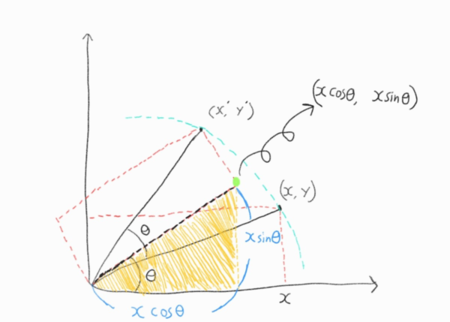
이제 이 회전하여 놓인사각형의 초록색 꼭짓점을 보면,
그 회전이동한 사각형의 밑변의 길이는 보라색 선을 통해 이동한 것이니까 $x$가 된다
여기서 다시 주황색 직각삼각형을 생각해보자
주황색 삼각형의 빗변의 길이가 x랑 같으니까 자연스럽게 밑변은 \(xcos \theta\)가 되고, 높이는 \(x sin \theta\)가 되며 그 점의 좌표는 (\(x cos \theta\), \(x sin \theta\))가 된다. 아래는 결과 사진과 시뮬레이션.gif다.
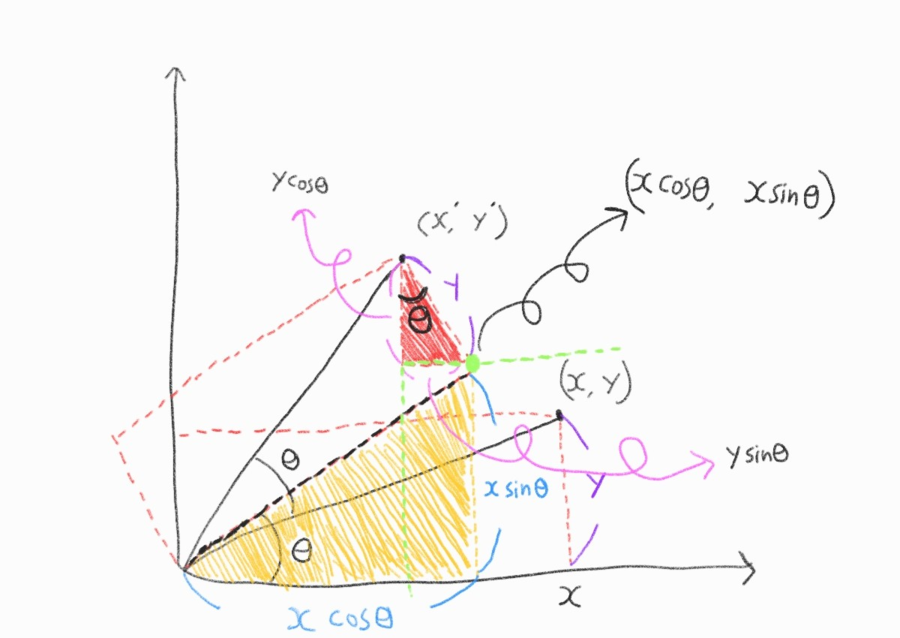
마지막으로 (\(x’, y’\))의 좌표를 찾기위해 아래의 빨간색 직각삼각형을 생각해보자
이는 아래 주황색 삼각형과 닮음이다.
왜냐하면 회색 수평선을 그엇을 때 생긴 \(\theta\)각과 합쳤을 때 양쪽 각각 직각이 되기 때문이다.
그리하여 자연스럽게 주황색 삼각형의 모든 각이 빨간색 삼각형의 각들과 닮음으로 일치한다
빨간색 직사각형은 회전이동을 한것이라 둘다 크기와 길이가 똑같다
$ \color{pink}{\Rightarrow} $ 자연스럽게 빨간 삼각형 빗변의 길이는 y가 된다
여기서 sin cos 계산하면 $x’$, $y’$의 위치 좌표 값을 계산할 수 있다
아래는 결과 사진과 시뮬레이션.gif다.
$x’$, $y’$를 계산해보면 아래와 같이 나온다
\(x’ = xcos \theta - y sin \theta\)
\(y’ = x sin \theta + y cos \theta\) $ \color{red}{\Rightarrow} $ \(\begin{pmatrix} x' \\ y' \end{pmatrix} \rightarrow \begin{pmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\)
이는 선형대수학의 회전행렬과 복소수의 오일러공식에 연계되는데 추후 관련 글을 올릴 것이다