오일러공식의 기하학적 설명
🙅♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다
1
2
3
4
5
<목차>
1. 들어가며
2. 오일러공식의 기하학적 의미
3. 결론
1. 들어가며
이번 글에서는 오일러 공식의 기하학적인 의미에 대해 알아볼 것입니다.
혹시 위의 슬라이드를 움직였을 때 아예 감이 안잡히신다면,
아래의 링크들을 참고하고 다시 보시면 쉽게 이해되실 것입니다
📐미분 방정식을 이용한 오일러공식 유도
📐회전변환의 기하학적인 이해
2. 오일러 공식의 기하학적 의미
$e^{i \theta} = cos \theta + i sin \theta$
위는 오일러 공식이다
참! \(e^{i \cdot 2\pi} = cos (2\pi) + i (sin 2\pi)\)면 360도니까 한바퀴 다 돈다
우변으로부터
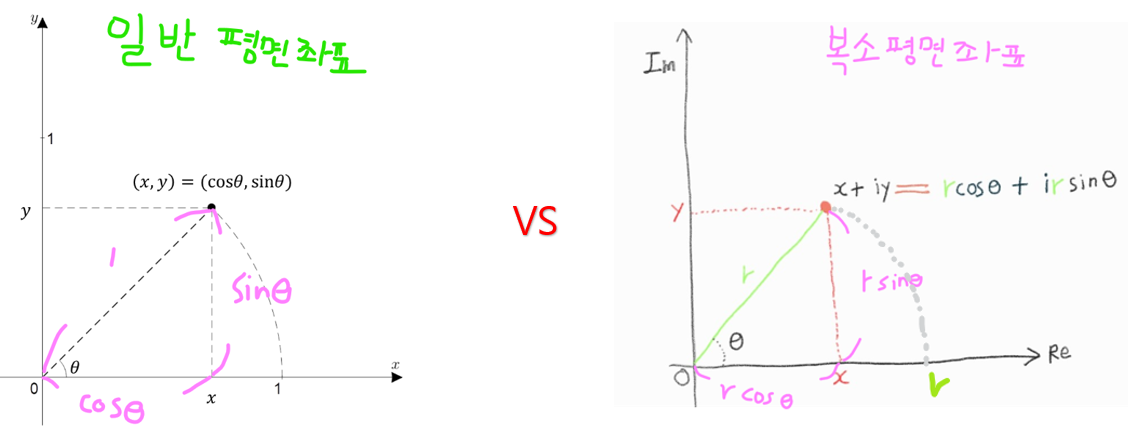
우변에 있는 $cos \theta + i sin \theta$에서 $cos \theta$와 $sin \theta$를 각각 $x$, $y$로 놓고 생각해보면
$e^{i\theta}$를 복소수라고 생각하여 아래처럼 식을 고칠 수 있다
$ \color{pink}{\Rightarrow} $ $e^{i\theta} = x+iy$
여기서 그 복소수\(\color{red}(\) \(e^{i\theta}\) \(\color{red})\)가 길이가 1인 막대가 실수축으로부터 \(\theta\)라디안 만큼 회전한 곳에 위치하는 값이라는 의미를 갖는다
우측의 그림을 보면 알 수 있듯이, 복소 평면 상에서 표현한 $x+iy$는
삼각함수로 표현하면 x축으로부터의 각도를 theta 라디안이라 했을 때
반지름인 r의 길이를 통해 $r cos(\theta) + i r sin(\theta)$다.
좌변으로부터
$e^{i\theta}$라는 것이 복소수이며, 반지름(r)을 1로 임의 설정하자
이 복소수는 길이가 1인 막대가 실수축으로부터 $\theta$라디안만큼 회전한 곳에 위치하는 값이라는 의미를 찾을 것이라는 걸 염두에 두도록 하자.
일단 자연상수 $e$의 정의부터 생각해보면 아래와 같다
\(e = \lim_{n\to \infty}\left(1+\frac{1}{n}\right)^n\)
그러면 자연상수 \(e\)에 지수 \(x\)승이 붙은 경우는??
\(e^x = lim_{n \to \infty} \left( 1+ \frac{x}{n} \right)^n = \left[\lim_{n\to \infty} \left(1+\frac{x}{n}\right)^{n/x}\right]^x\)
잠시 참고!
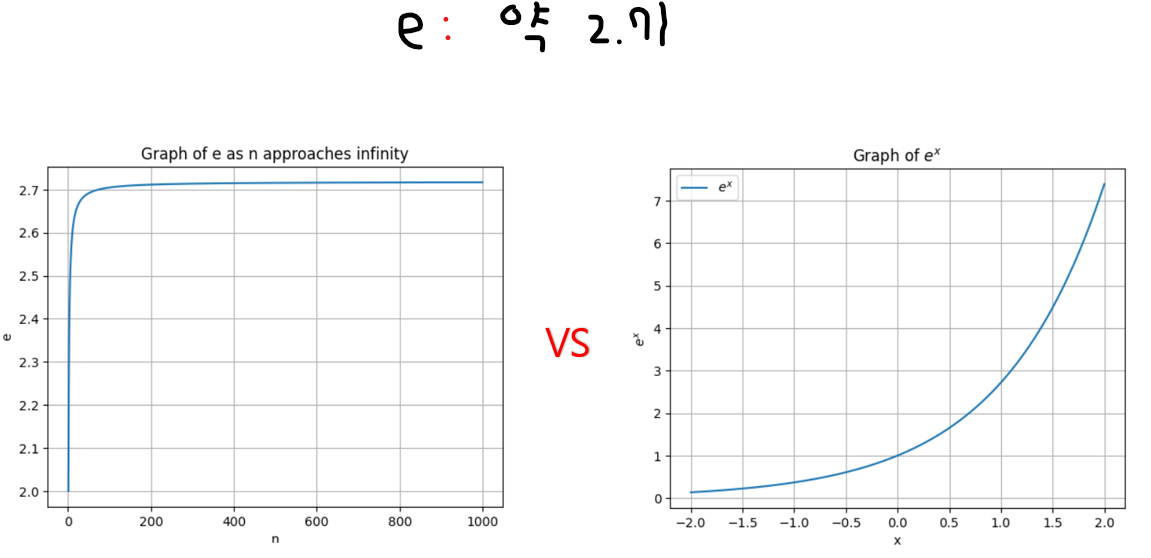
블로그 주인장이 수학을 너무 몰라서 $e$랑 $e^x$가 눈으로 안그려져 그래프를 추가했다
이미 아는 분들은 그냥 넘어가도 좋을 것 같다
위의 그래프를 보면 e에 대해 훨씬 더 이해가 잘 되었을 것이다.
아까 내용에서 이어서 하자면, 지수 $x$승 대신에 허수지수인 $i$승으로 바꾸면 어떨까?
\(e^i = lim_{n \to \infty} \left( 1+ \frac{i}{n} \right)^n = \left[\lim_{n\to \infty} \left(1+\frac{i}{n}\right)^{n/i}\right]^i\)
위의 식에서 이 부분만 보자 \(\color{pink}{\Rightarrow}\) \(lim_{n \to \infty} \left( 1+ \frac{i}{n} \right)^n\)
자연상수에 붙은 허수 지수: 호(arc) 위의 점
어? 위에는 \(lim_{n \to \infty}\)인데 n=1부터 보면 어떨까?
(i를 1로 생각하자)
n=1
\(\text{n=1 }$ **$ \color{pink}{\Rightarrow}\)** \(\left(1+\frac{i}{1}\right)^1\)
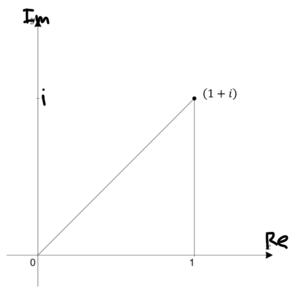
이것은 $1+i$라는 복소수를 의미하며, 이때 real(실수부), Im(허수부)를 나누면 \(\Rightarrow\) \(x, iy\)좌표는 (1, i)
이 좌표의 길이 \(\color{pink}{\Rightarrow}\) \(|1+i| = \sqrt{(1+i)(1-i)} = \sqrt{2} \approx 1.4\)
복소평면 상에서 표현하면 아래와 같다
n=2
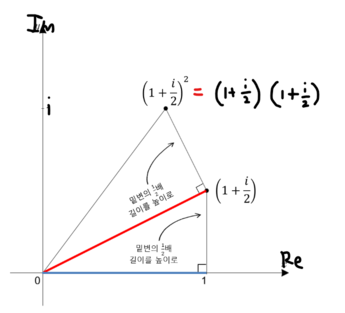
$\text{n=2}$ \(\color{pink}{\Rightarrow}\) \(\left(1+\frac{i}{2}\right)^2 = \left(1+\frac{i}{2}\right)\left(1+\frac{i}{2}\right) = 0.75+i\)
어? \(\left(1+\frac{i}{2}\right)\left(1+\frac{i}{2}\right)\) 이게 뭔말이지?
한마디로 설명하면 \((1+\frac{i}{2})\)를 그려서 얻은 직각 삼각형에 대해,
그 빗변의 길이 \(\frac{1}{2}\)의 높이로 하는 직각삼각형을 한번 더 그림
x, iy 좌표는 실수부, 허수부를 나누어 –> (0.75, i)
이 좌표의 길이 \(\color{pink}{\Rightarrow}\) \(|0.75+i| = \sqrt{(0.75+i)(0.75-i)} = \sqrt{1.5625} \approx 1.25\)
(아래 그림 참고)
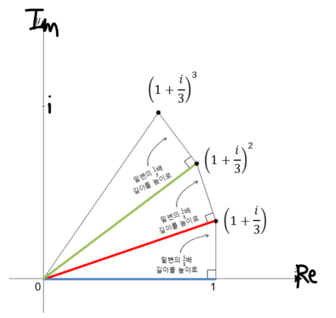
n=3
3. 결론
n이 커지면 커질 수록 1과 \(\frac{1}{n}\)을 밑변과 높이로 하는 직각 삼각형의
빗변의 길이(원점에서 부터의 x,y 좌표 길이)는 작아지면서 거의 1에 가까워지며,
n이 커질 수록 반지름이 1이고, 길이가 1인 호(arc) 위의 점에 가까워지는 것을 알 수 있다.
아래 시뮬레이션을 움직여보고 gif사진을 보면 n이 커질수록,
허수 축인 i 즉 y축의 1에 가까워지는 것을 알 수 있다
(여기서는 복소평면좌표라 1을 i로 대신 표시했다)