Heap

목차

🎱힙 자료구조?
	잠깐! 완전 이진트리란?

1. 힙 자료구조는 언제 사용?
2. 힙 자료구조의 종류
3. 최소 힙 자료구조 동작 과정
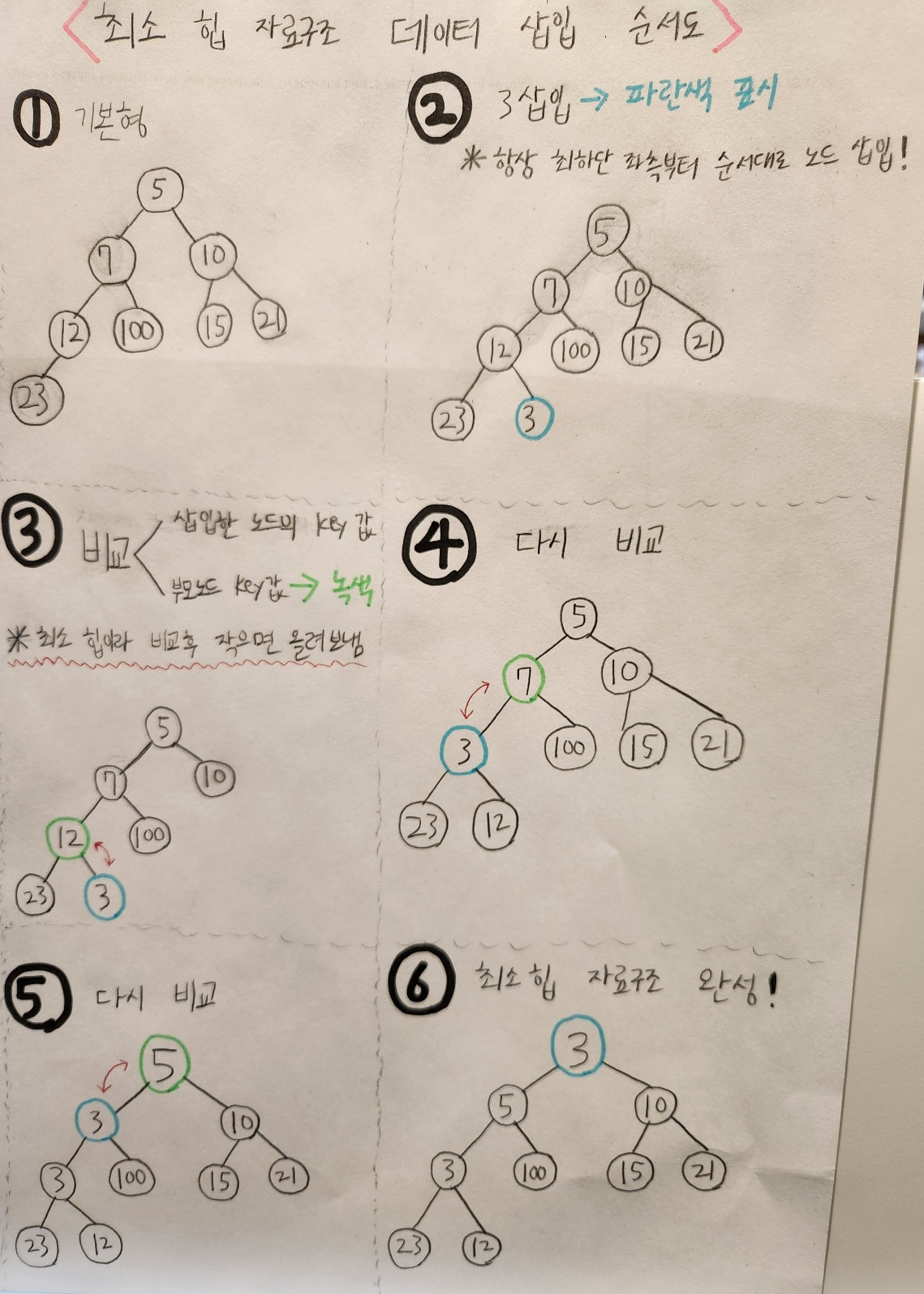
	1) 데이터 삽입
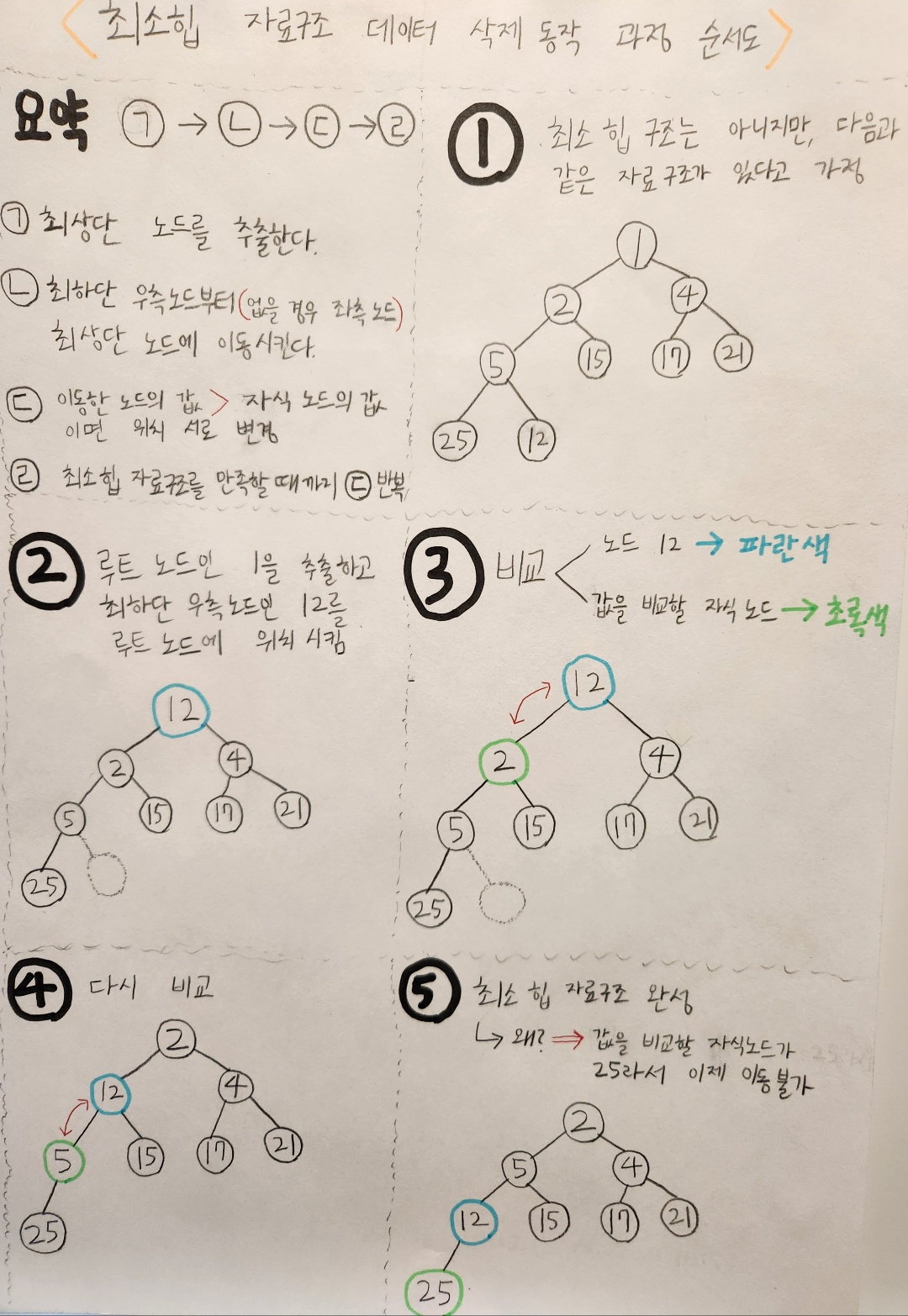
	2) 데이터 삭제
4. 구현 실험(python)

🎱힙 자료구조?

가장 높거나 가장 낮은 우선순위 예시로 최대 or 최소값 을 가지는 노드를 찾아내기 위해 고안된 *완전 이진트리(Complete Binary Tree)에 기반한 자료구조다

따라서 가장 높거나 가장 낮은 우선순위를 가지는 노드가 루트노드(가장 최상단)에 온다.

잠깐! 완전 이진트리란?

• 각 노드가 최대 최대 2개의 자식노드를 갖는 트리 형태의 자료구조
• 최하단을 제외한 모든 노드는 채워져있어야 한다
• 노드를 삽입할 때 최하단 좌측부터 삽입해야한다.

1. 힙 자료구조는 언제 사용?

• N개의 데이터가 저장된 리스트에서 최댓값 또는 최솟값을 탐색하려면 O(N) 만큼의 시간이 필요한데, 반면 힙 자료구조는 ***O(logN)*** 만큼의 시간이 필요하다.
• 최댓값 or 최솟값을 빠르게 탐색해야 하는 우선순위 큐, 최단 경로 알고리즘 등을 구현할 때 좋다

2. 힙 자료구조의 종류

• 최대 힙: 부모 노드 값 > 자식 노드 값
• 최소 힙: 부모 노드 값 < 자식 노드 값

3. 최소 힙 자료구조 동작과정

1) 데이터 삽입

2) 데이터 삭제

4. 구현 실험(python)

• heapq 세팅

import heapq
# 파이썬에 내장된 heapq 라이브러리로 최소 힙 자료구조 구현 가능

joonhwan_heap = []
# 힙 생성

• 힙 데이터 삽입 heappush

heapq.heappush([힙 이름], [추가할 원소])
# heappush를 사용하면 최소 힙 자료구조를 유지하면서 새로운 원소를 추가할 수 있다.

#------------ 아래는 예시 ----------------------------------------------
heapq.heappush(joonhwan_heap, '2')
heapq.heappush(joonhwan_heap, '5')
heapq.heappush(joonhwan_heap, '1')
heapq.heappush(joonhwan_heap, '3')
heapq.heappush(joonhwan_heap, '6')
heapq.heappush(joonhwan_heap, '4')

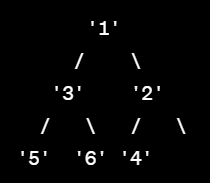
print(joonhwan_heap)
# 결과: ['1', '3', '2', '5', '6', '4']

• 힙 데이터 삭제

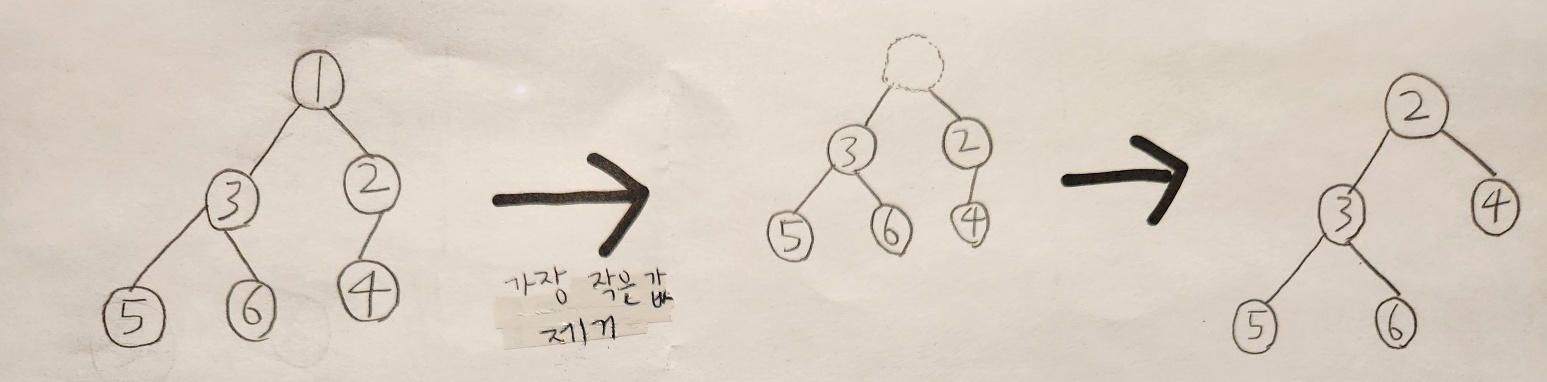
heapq.heappop([힙 이름])
# 우선순위가 가장 높은 데이터를 삭제한다. --> 여기서는 최소 힙이라 루트노드를 삭제할 것이다.

print(heapq.heappop(joonhwan_heap))
# 결과: 1

print(joonhwan_heap)
# 결과: ['2', '3', '4', '5', '6']

참고

https://heytech.tistory.com/69