lagrangian multiplier
🙅♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다
1
2
3
1. 들어가며
2. 에니메이션 설명
3. 참고
1. 들어가며
(대부분의 영상과 사진은 상우쌤의 수학노트 에서 퍼왔습니다. 선생님 덕분에 쉽게 이해할 수 있었습니다 유용한 자료 공유해주셔서 정말 감사합니다)
요약:
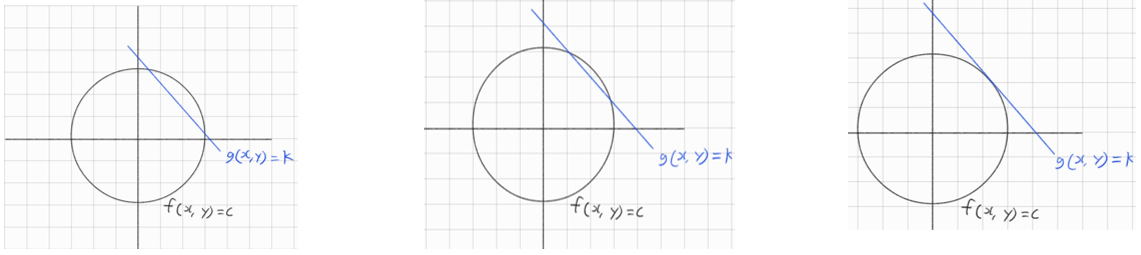
최적화문제는 반드시 조건이 있어야하고, 그 예로 g(x,y)=k을 통해
f(x,y), g(x,y)가 접할 때 f(x,y)의 극댓값 or 극솟값이 형성되는데
그때 min value나 max value를 찾을 수 있게 된다.
2. 에니메이션 설명
이변수함수 \(f\)로 이루어진 산이 있다고 가정하자
\(f(x,y)=4-x^2-2y^2\)
산에 등산로를 내기위해 지도를 펼치니 아래 그림처럼 같아졌고 예상경로 \(g(x,y)\)를 그렸다
\(g(x,y)=2(x-1)^2-10y+3=0\)
⁉️질문
이 예상경로를 따라 올라갔을 때 최고 높이가 얼마일까?
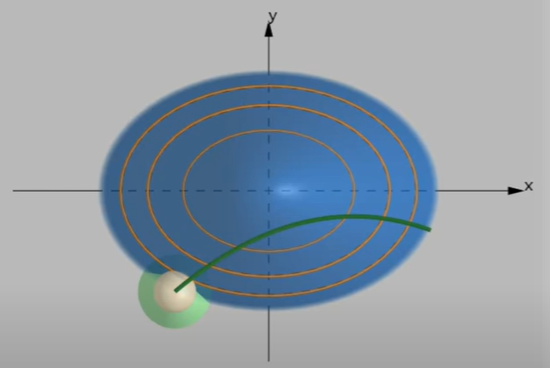
자 그러면 다시 저 눕힌 모형을 세워보면 실제 등산로는 xy평면에 수직인 곡면과 만나는 선이 된다
아래 그림은 예상경로에 대한 실제 등반 가능한 경로를 평면으로 나타낸 것이다
아래 영상은 예상경로로 올라가서 최고점(최대값)으로 가는 것을 나타낸 것이다
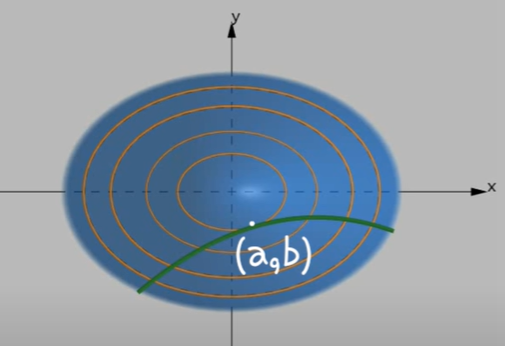
😎ㅇㅎ 사람이 제일 꼭대기에 올라갔을 때가 최고높이니 그걸 등고선에서 찾으면 되겠네
그리고 그 최고높이는 f(x,y)와 g(x,y) 두 곡선이 접할때겠군
여기서 접점 a, b를 각각 함수 f랑 g에 대입하면 높이가 나오고
그 접점을 찾는 과정이 바로 라그랑주 승수법 이다
여기서 높이를 같게 하려면 어떻게 구할 수 있을까?
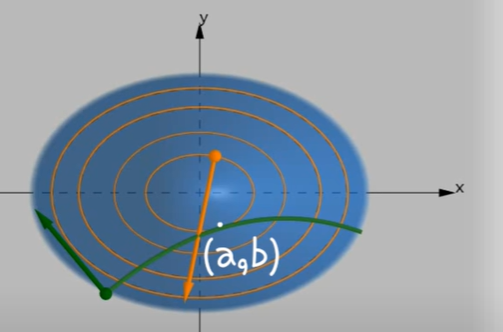
이 그림은 각각의 두 곡선의 공통접선에 수직인벡터를 표시한 것인데,
같은 높이로 만드려면 기울기벡터(gradient vector)의 방향이 같게 하자
아래 그림을 참고하자
이 그림을 보면 2개의 gradient vector가 높이는 다르지만 같은 방향일 때가 있다
그때 만족하는 두 식은 아래와 같다
*참고 \(\bigtriangledown\)는 gradient vector 즉 기울기를 나타낸다
\(g(a,b)=0 \\ \bigtriangledown f(a,b)=\gamma \bigtriangledown g(a,b)\)
이때 두 식을 연립방정식으로 찾으면 된다는 것이다
근데 두 기울기벡터(gradient vector)의 방향은 같아도 크기는 다를 수도 있으니까 차이를 맞추기 위해 \(\gamma\)를 곱해주는데 이게 라그랑주 승수다