limit

🙅‍♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다

<목차>

1. 극한
 1-1 함수 극한의 수렴
 1-2 극한 기초문제 예시 (4개)

1. 극한

1-1 함수 극한의 수렴

함수 \(f(x)\)에서 (1) \(x \neq a\)이면서, \(x\)가 \(a\)에 한없이 접근할 때,
(2) \(f(x)\)의 값이 일정한 값 L에 한없이 가까워지면
“\(x \rightarrow a\)일때 \(f(x)\)는 L에 수렴한다”라고 정의한다.

기호로는 \(\lim_{n\rightarrow \infty} f\left(x \right) = L\) 이라 표현하고 L을 \(f(x)\)의 극한값이라 한다

(1) x가 a에 한없이 접근할 때 의미 ?? \(\Rightarrow\) \(\begin{cases} x \rightarrow a^- \\ x \rightarrow a^+ \end{cases}\)

좌극한(x가 a보다 작은 값에서 접근할때)랑,
우극한(x가 a보다 큰 값에서 접근할 때)이다
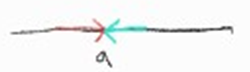
참고로 극한은 좌극한 = 우극한 이어야 성립한다.

이것을 보고 알 수 있는 것은
\(\lim_{x \rightarrow a^-} f\left(x \right) = L\)이고,   \(\lim_{x \rightarrow a^+} f\left(x \right) = L\)일 때
\(\lim_{x \rightarrow a} f\left(x \right) = L\)이 된다

why? \(\Rightarrow\) 어차피 방향은 다른 곳에서 접근해도 수렴하는 값은 같기 때문이다

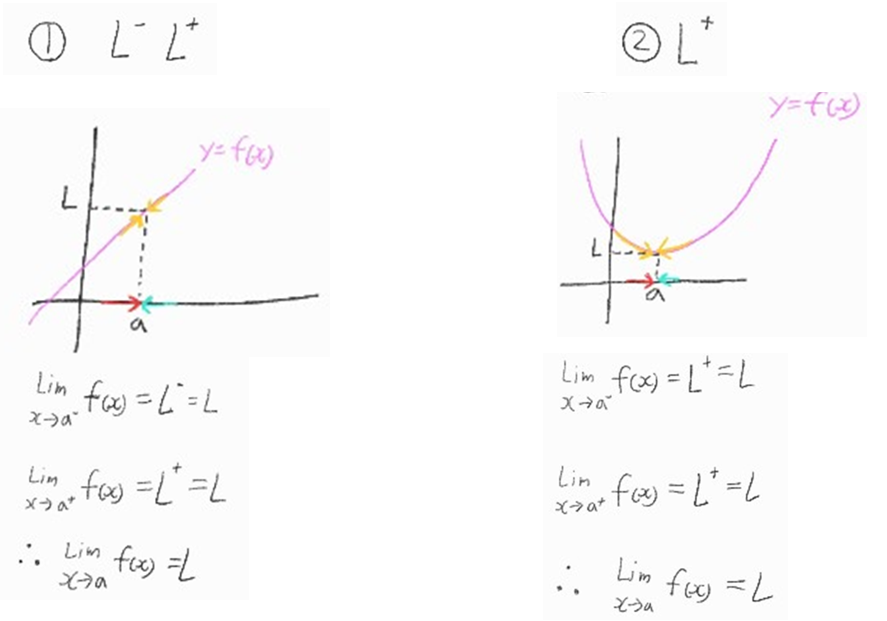
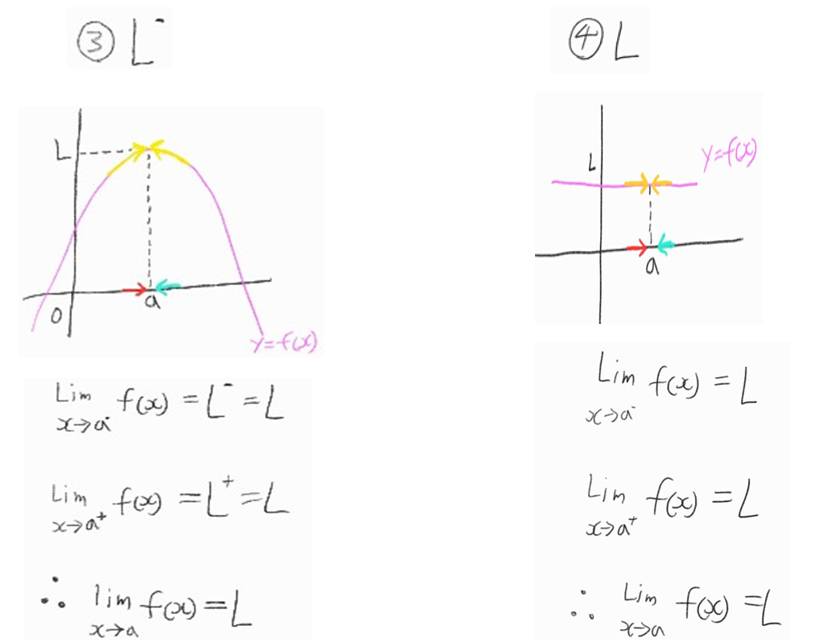
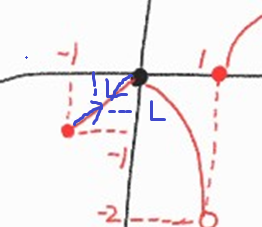
(2) f(x)의 값이 일정한 값 L에 한없이 가까워지면의 의미?? 아래 극한의 수렴 예시 4가지 들을 살펴보자

위의 각 그림에서 \(L^-\), \(L^+\)는 L보다 작은 곳과 큰곳에서 접근한 것을 나타내는 것이고,
\(L^+\)는 L보다 큰 곳에서 작은쪽(아래쪽)인 \(L\)로 접근한 것
\(L^-\)는 L보다 작은 곳에서 큰 곳인 \(L\)로 접근한 것

(4)번의 \(L\)은 (1), (2), (3)처럼 수렴이 아니라 말 그대로 L 그 자체인 것이다.

1-2 극한 기초문제 예시 (4개)

다음 극한 값을 계산하라
1) \(\lim_{x \rightarrow 2} \left[ x \right]\)

sol-1:

좌극한 = \(1<x<2\) 이기에 \(\lim_{x \rightarrow 2^-} \left[ x \right] = 1\)

우극한 = \(2<x<3\)이기에 \(\lim_{x \rightarrow 2^+} \left[ x \right] = 2\)
즉 좌극한 \(\neq\) 우극한이므로 극한값이 없다.

2) \(\lim_{x \rightarrow 0} \frac{ \vert x \vert }{x}\)

sol-2:
좌극한 = \(x <0\) 이라 \(\lim_{x \rightarrow 0} \frac {-x}{x} = -1\)
우극한 = \(x > 0\) 이라 \(\lim_{x \rightarrow 0} \frac {x}{x} = 1\)
즉 마찬가지로 좌극한 \(\neq\) 우극한이므로 극한값이 없다.

3) 정의역이 \(\{x \vert \quad -1 ≤ x ≤ 3\}\) 인 함수 \(y=f(x)\)의 그래프가 그림과 같을 때 아래 보기에서 옳은 것을 모두 고른 것은?

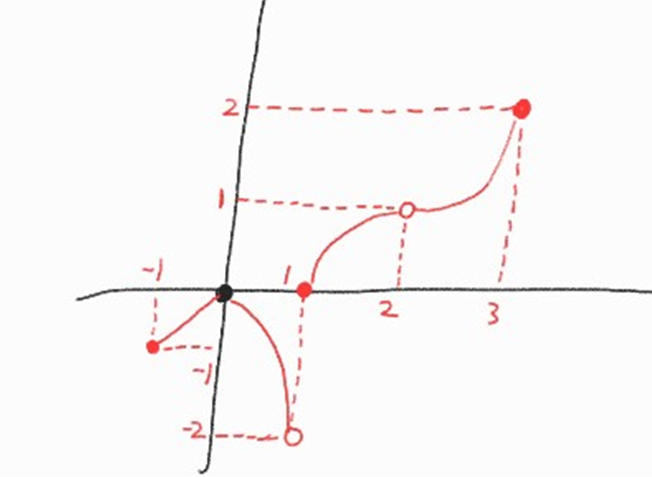
-------------------보기--------------------
ㄱ \(\lim_{x\rightarrow 1} f\left(x \right)\) 가 존재한다

ㄴ \(\lim_{x\rightarrow 2} f\left(x \right)\)가 존재한다

ㄷ \(-1<a<1\) 인 실수 a에 대해 \(\lim_{x\rightarrow a} f\left(x \right)\)가 존재한다.
-------------------------------------------

sol-3:
ㄱ의 경우 좌극한에서는 \(\lim_{x\rightarrow 1^-} f\left(x \right) = -2^+\)인데 이게 무슨말이냐면 -2보다 조금 더 작은 숫자로 되어 -2.xx 이렇게 될 수도 있다는 얘기다 아무튼 좌극한값은 -2가 된다
우극한에서는 \(\lim_{x\rightarrow 1^+} f\left(x \right) = 0\) 이므로 좌극한 \(\neq\) 우극한이라 극한값이 없다

ㄴ의 경우 좌극한, 우극한 둘다 1로 수렴하기에 당연히 극한이 1로 존재한다
ㄷ의 경우 a가 -1과 0 사이에 있다고 생각해보자
아래의 그림을 통해 쉽게 보자

수렴하여 극한값은 존재하고 그 값은 L이다
\(\color{red}{\therefore}\) 답은 ㄴ, ㄷ

4) \(\lim_{n \to \infty} \left(1+\frac{x}{3}\right)^{\frac{1}{x}}\) 풀어라

sol-4:
\(\lim_{n \to \infty} \{ \left(1+\frac{x}{3}\right)^{\frac{3}{x}} \}^{\frac{1}{3}}\)
여기서 \(중괄호^{\frac{3}{x}}\)까지 e랑 같은 말이기 때문에 답은 \(e^{\frac{1}{3}}\)가 되는데 이렇게도 바꿀 수 있다 \(\sqrt[3]{e}\)

참고

1. 큐스터디 전공수학 - 대학수학의 기초/ 미적분 강의 (3시간)
2. 제9장: 넓이와 기울기 사이 숨겨진 연결고리 미적분학의 본질
3. eo 미적분 기초부터