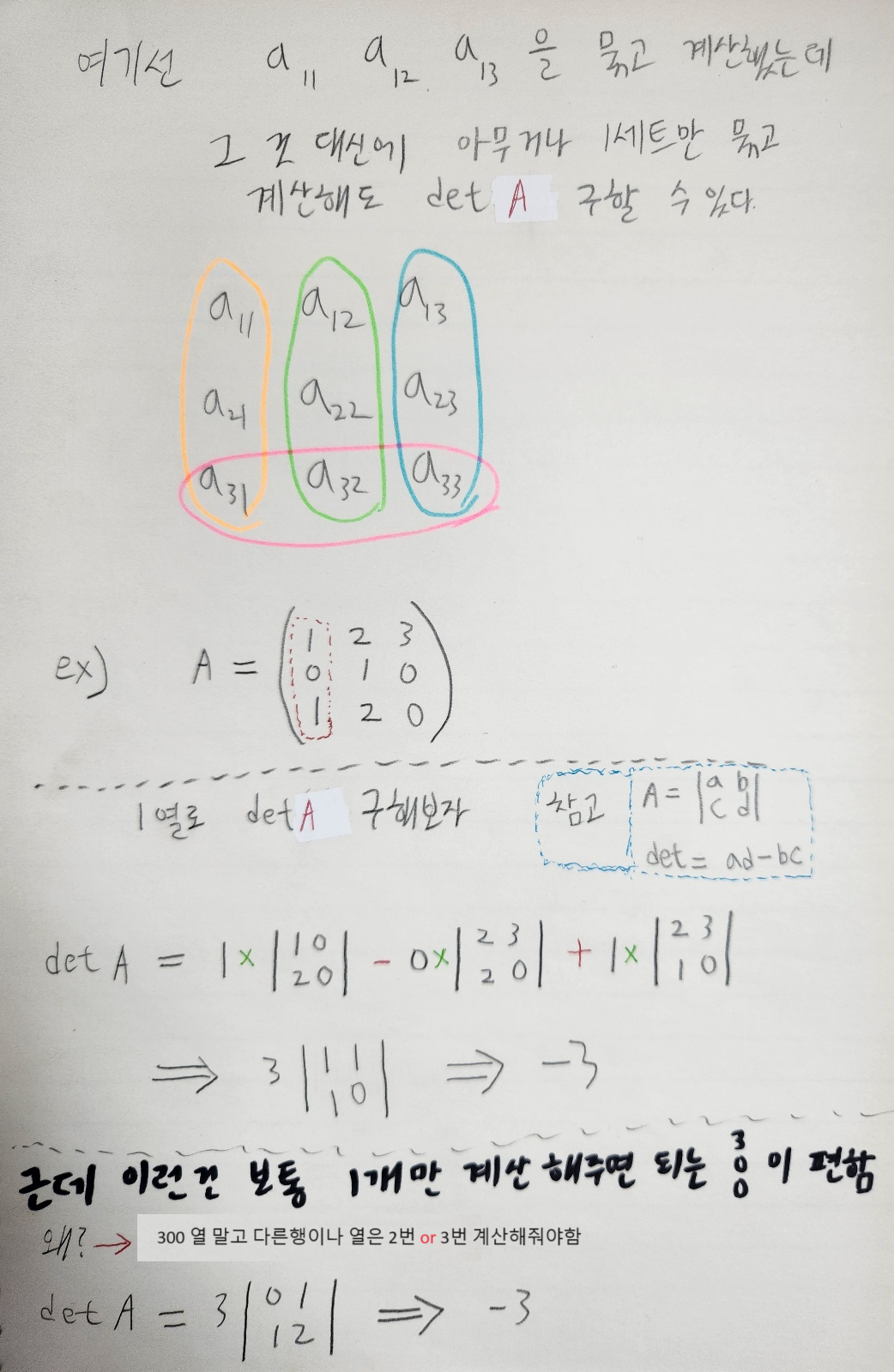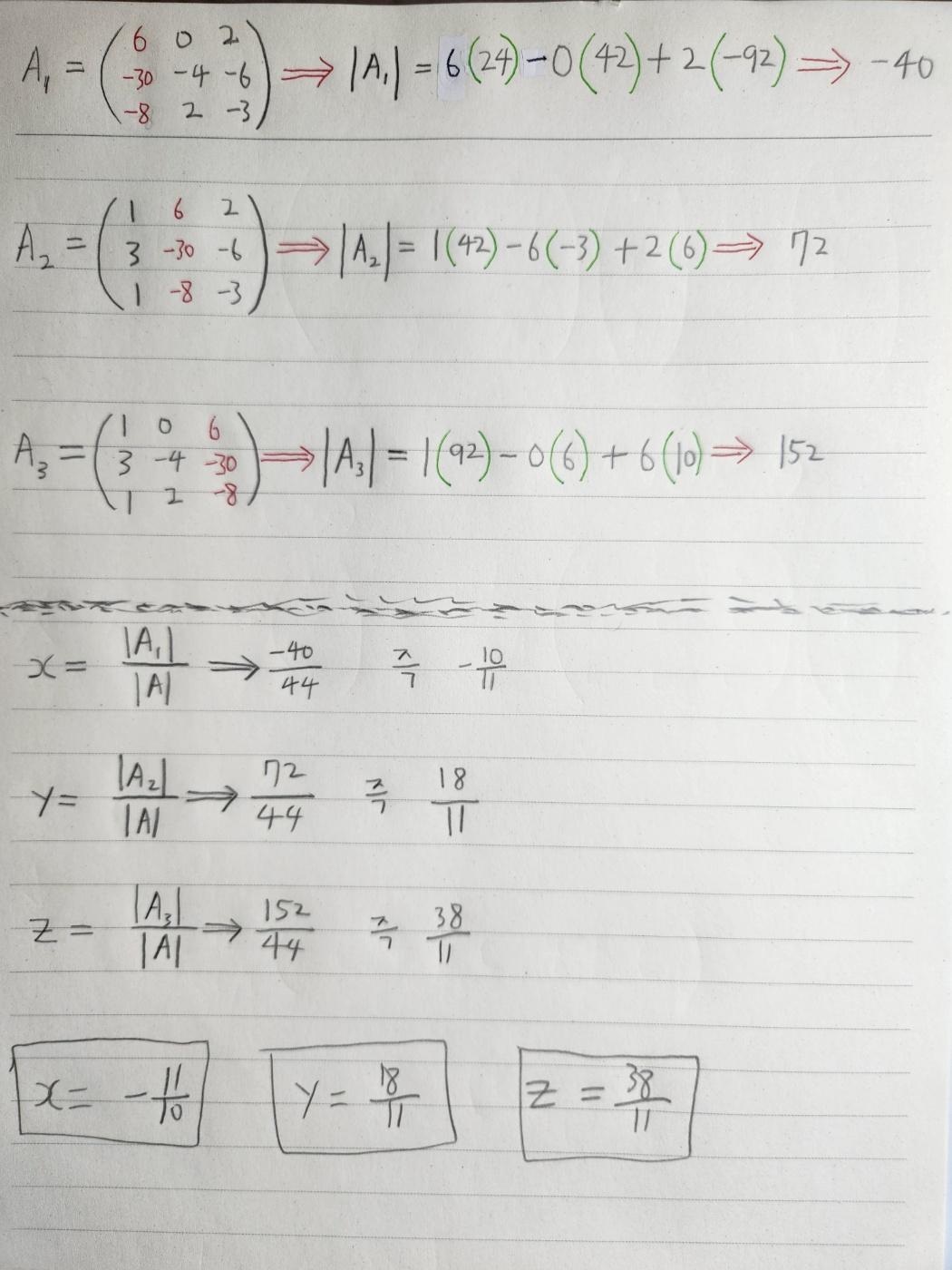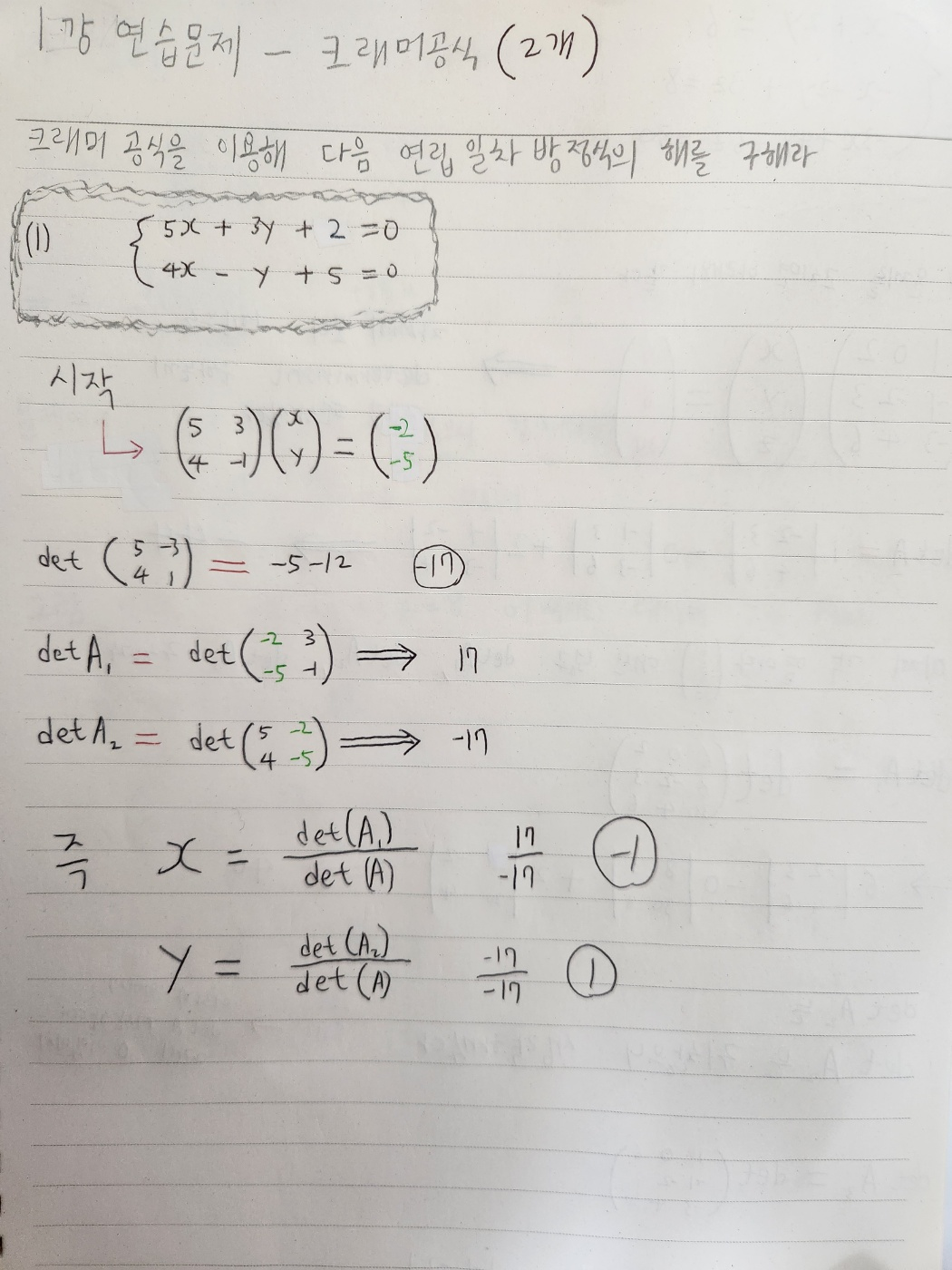[선형대수학] 1강 행렬과 행렬식
🙅♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다
목차
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
* 간단한 정리
0. 선형대수학을 배우는 이유?
1. 행렬
1-1 용어정리
1-2 행렬의 연산
2. 연립일차방정식
2-1 행렬의 표현
2-2 가우스 조던 소거법 & 예제
3. 행렬식
3-1 행렬식이란? & Sarrus 전개
3-2 역행렬
3-3 Crammer`s Rule
3-4 Crammer`s Rule 예제 1개
4. 이벤트문제 + 연습문제
!이벤트 문제
4-1 가우스 조던 소거법
4-2 역행렬
4-3 크래머공식으로 연립일차방정식 해 구하기(2개)
*간단한 정리
1
2
3
2x+3y = 7
4x-y = 5
위의 식 2개를 통해 AX=B 선형시스템으로 어떻게 나타낼까?
\(A = \begin{bmatrix} 2 & 3\\ 4 & -1 \end{bmatrix}, \quad X = \begin{bmatrix} x\\ y \end{bmatrix}, \quad B = \begin{bmatrix} 7\\ 5 \end{bmatrix}\)
A = 계수행렬, X = 변수를 포함한 열벡터 B = 상수벡터
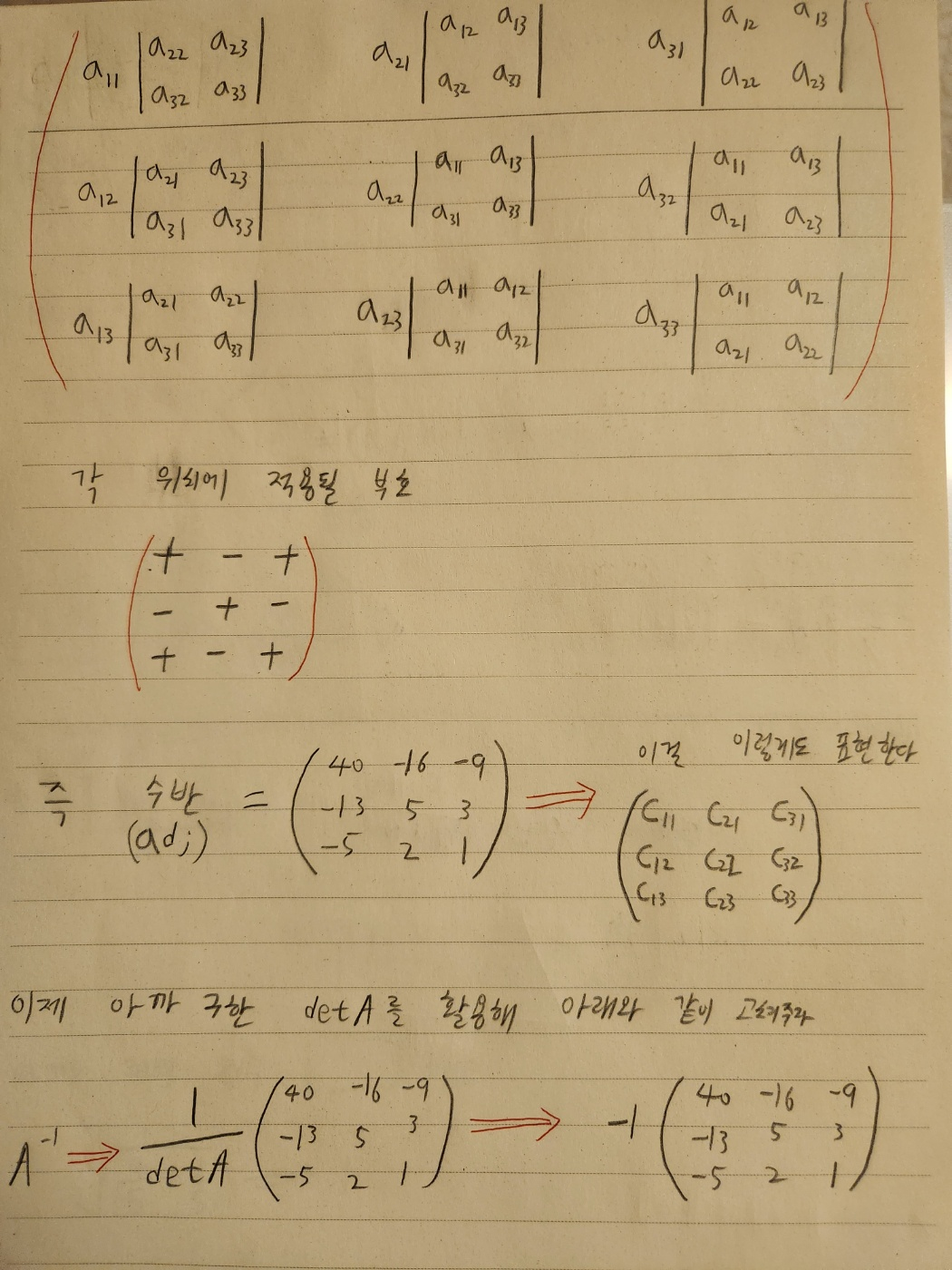
해를 구하기 위해 X = \(A^{-1}B\)를 만들어주어야 합니다
잠깐!
역행렬 공식
\(A^{-1} = \frac{1}{det(A)}adj(A)\)
을 참고하자
det(A)=(2×(−1))−(3×4)=−2−12=−14
수반 행렬(adjugate) = \(adj(A) = \begin{bmatrix} -1 & -3\\ -4 & 2 \end{bmatrix}\)
따라서 역행렬은 다음과 같습니다
\(A^{-1} = \frac{1}{-14} \begin{bmatrix} -1 & -3\\ -4 & 2 \end{bmatrix} = \begin{bmatrix} \frac{1}{7} & \frac{3}{14}\\ \frac{2}{7} & -\frac{1}{7} \end{bmatrix}\)
이제 상수벡터 B에 곱합니다 \(X = A^{-1}B = \begin{bmatrix} \frac{1}{7} & \frac{3}{14}\\ \frac{2}{7} & -\frac{1}{7} \end{bmatrix} \begin{bmatrix} 7\\ 5 \end{bmatrix} = \begin{bmatrix} \frac{7}{7} + \frac{15}{14}\\ \frac{14}{7}-\frac{5}{7} \end{bmatrix} = \begin{bmatrix} \frac{29}{14} \\ \frac{9}{7} \end{bmatrix}\)
이런식으로 X의 해를 구했고 이제 위의 선형방정식에 검증하면 됩니다!
0. 선형대수학을 배우는 이유?
공간이라고 생각하면 직관이 먹힌다
이 세상은 3차원의 공간으로 되어있으며, 사람들이 살아가는 이 공간을 표현하고 기술하기 위해 벡터의 무대인 선형대수는 공간을 설명하기에 편리합니다
- 근사 수단으로 사용하기 편리
- 기계학습
1. 행렬
1-1. 용어정리
*차원 계산법
행렬곱에서 \(A_{3*1} B_{1*3}\)이 있다하자
여기서 mxn은 행x열이니 위는 matrix \(AB_{3*3}\) 가 된다
1-2. 행렬의 연산
2. 연립일차방정식
2-1. 행렬의 표현
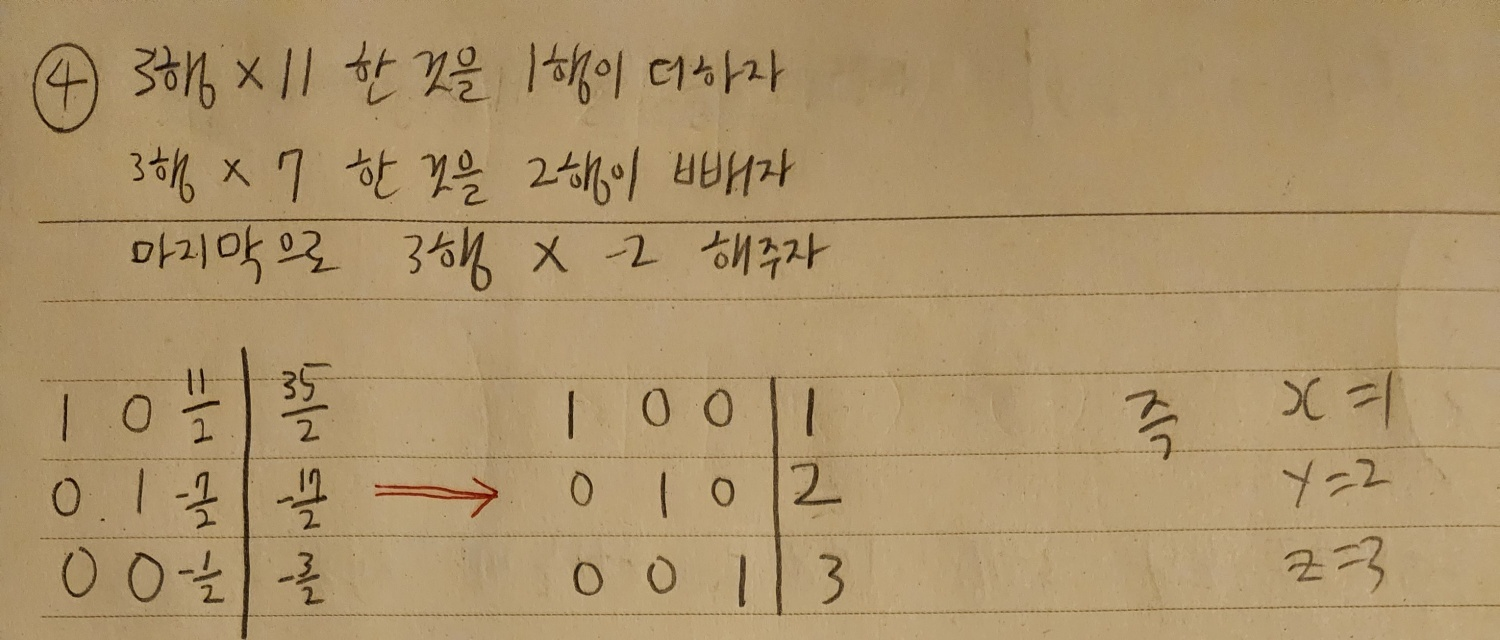
2-2 가우스 조던 소거법 & 예제
3. 행렬식
3-1. 행렬식이란? & Sarrus 전개
행렬식은 아래처럼 식을 계산하는 것을 의미합니다.
3-2. 역행렬
3-3. Crammer`s Rule
- 연립일차방정식 AX = B 에서 A가 행렬식 0이 아닌 정사각행렬일 때
3-4. Crammer`s Rule 예제 1개
4. 이벤트문제 + 연습문제
1
!이벤트 문제
\(A = (a_{ij})_{3*3}, \quad B=(_{ij})_{3*3}, \quad detA =-1, \quad detB = 2 \\ 일 때, det(3(AB))는?\)
————————————————-
$ \color{red}{\Rightarrow} $
위는 m x n 행렬의 문제입니다
A: 3x3, B: 3x3이니까
|A| = -1, |B| = 2
여기서 알아야하는 것은 3x3 이랑 3x3 곱하면 그대로 3x3행렬 나옵니다.
그리고 실수가 행렬식을 빠져나갈 때는 n승만큼 빠져나가야합니다
즉 |3(AB)| $ \Rightarrow $ \(3^3\)|AB| $ \Rightarrow $ \(3^3\)|A||B|가 됩니다
답을 계산하면 27 * -1 * 2 = -54
4-1. 가우스 조던 소거법
4-2. 역행렬
4-3. 크래머공식으로 연립일차방정식 해 구하기(2개)
