[선형대수학] 2강. 물리적 벡터
🙅♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다
목차
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
0. 핵심 요약
1. 벡터와 좌표계
1-1. 평면벡터
1-2. 공간벡터
1-3. n차원 벡터
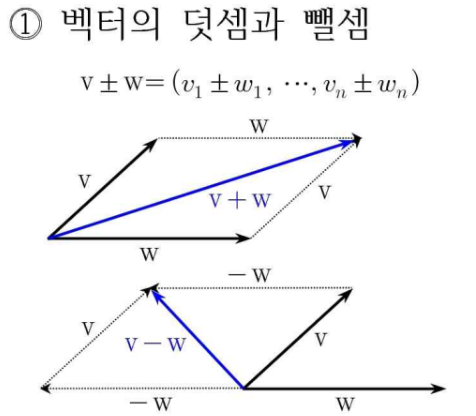
2. 벡터의 연산
2-1. Norm
2-2. 선형결합
2-3. 스칼라 곱 + cosine simmilarity
2-4. 벡터 곱
3. 벡터의 응용
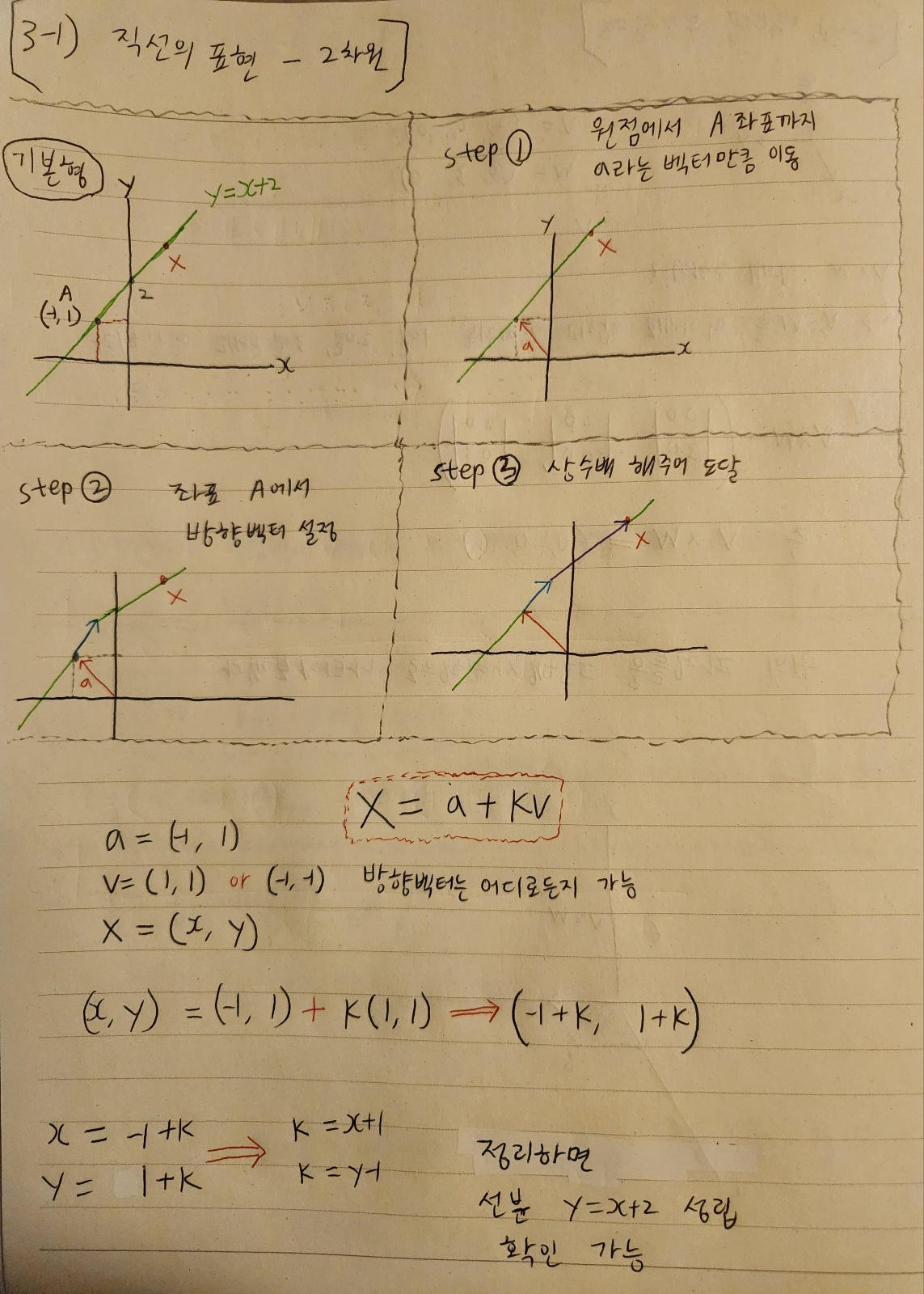
3-1. 직선의 표현
3-2. 평면의 표현
4. 행벡터와 벡터내적간의 연관성
5. 예제
5-1. cos theta
5-2. 두 벡터를 활용한 평행사변형 넓이
5-3. 직선과 평면이 동시에 만나는 좌표
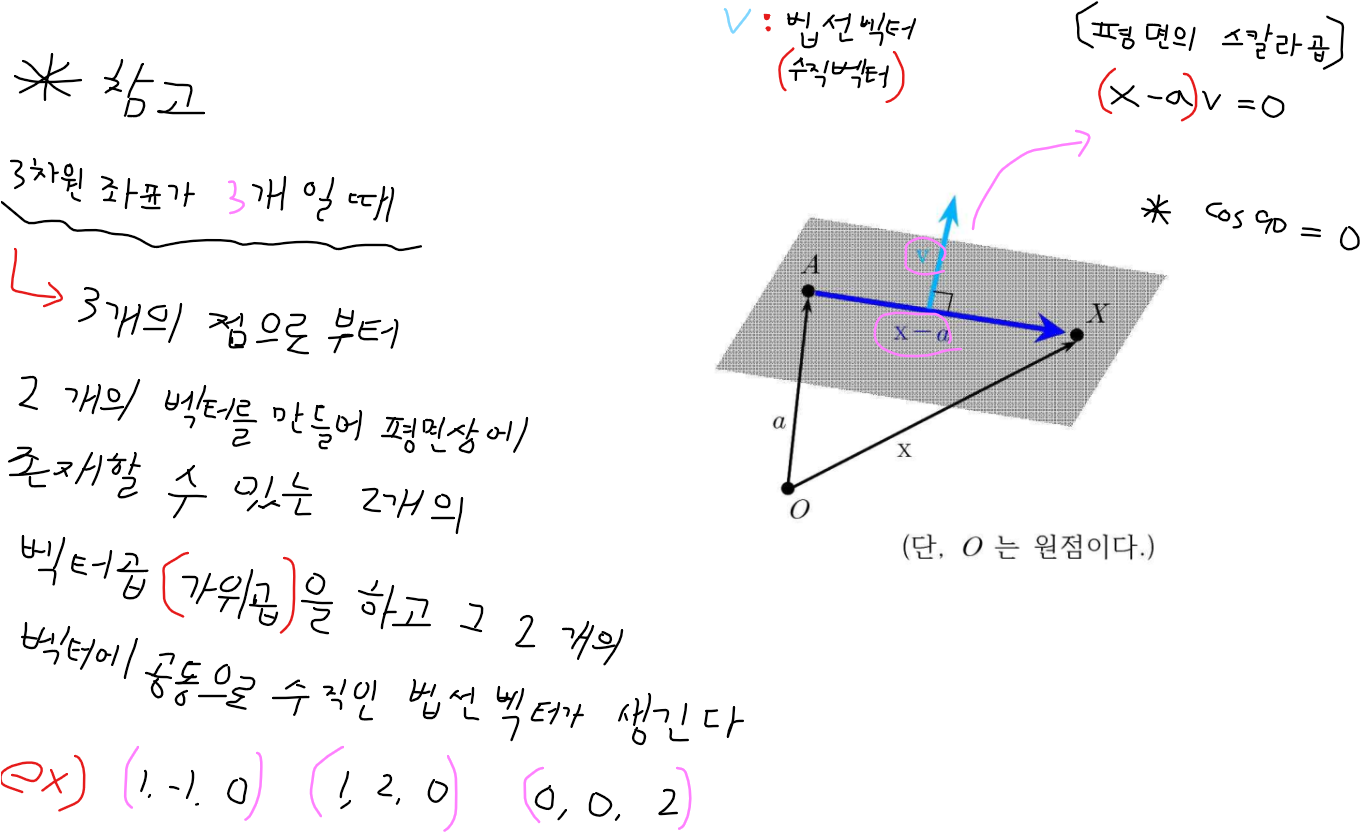
6. 참고
0. 핵심 요약 (3개)
norm(정규화) 쓰는 이유
\(\frac{a}{\sqrt{a^T a}} = \frac{a}{||a||}\) (크기가 1인 벡터)
벡터의 norm을 정규화하면 서로 다른 벡터들 간의 크기 비교가 쉽다
ex) 유클리드 노름을 사용하여 벡터의 길이를 계산하면 벡터 간의 거리를 비교 가능
벡터의 norm을 정규화하면 벡터의 방향을 유지하면서 크기를 조절할 수 있다
주로 벡터를 단위 벡터로 변환하여 특정 방향으로의 이동이나 변형을 측정할 때 사용
벡터의 내적 연산
\(\begin{bmatrix} a_1\\ a_2 \\ \vdots \\ a_n-1 \\ a_n \end{bmatrix} \cdot \begin{bmatrix} h_1\\ h_2 \\ \vdots \\ h_n-1 \\ h_n \end{bmatrix} = a_1h_1 + a_2h_2 + \ldots + a_{n-1} h_{n-1} + a_{n} h_{n}\)
즉 \(a \cdot h = \sum_{i=1}^{10} a_i h_i\)
ex) \(a\), \(b\), … \(z\) \(\in R^3\) 일 때 \(a\)과 \(h\)끼리 내적 가능
\(\color{pink}{\Rightarrow}\) \(a \cdot h = a_x h_x + a_y h_y + a_z h_z\) (벡터의 내적은 같은 공간 안에서만 가능하다!)
- 하나 더
n차 다항식 벡터공간과 \(R^n\) 벡터 공간으로 내적이 정의 되는가?
\(\Rightarrow\) 암 물론 \(f(a, b) = f(b, a)\)가 만족하면 된다
정사영
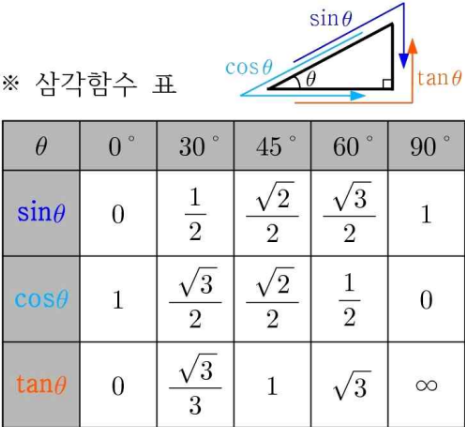
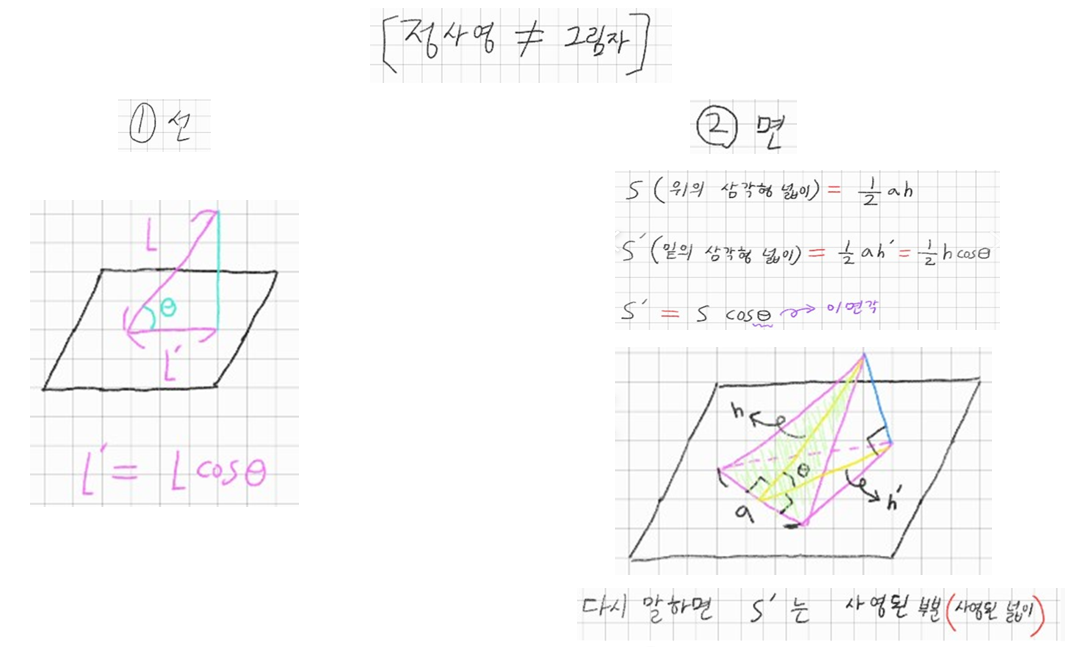\(\vec{a} \cdot \vec{b} = ||a|| \cdot ||b|| cos \theta\)
(\(\theta\)구하고 수선의 발을 내려 \(\perp\)표시하고 다시 확인해보면 자연스럽게 내적 이해가 될 것이다)
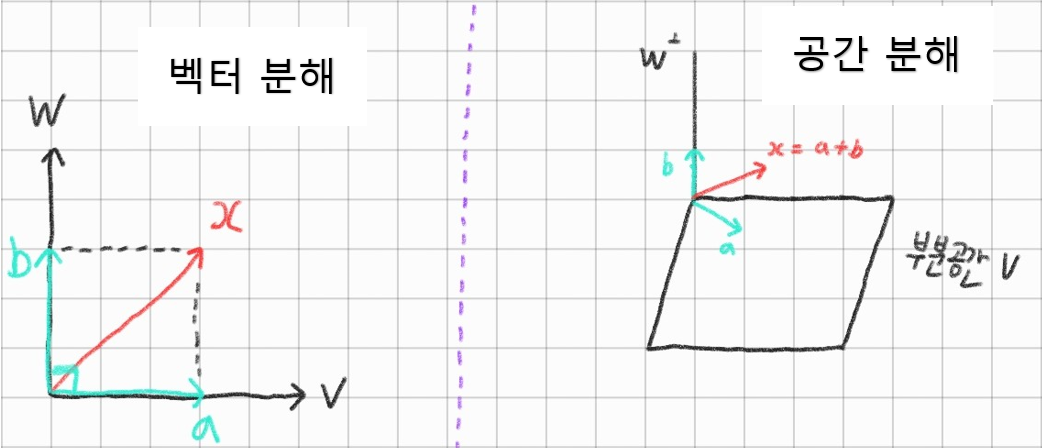
\(V \subseteq |R^n\), V는 부분공간일 때,
\(x \in |R^n\), \(x = x_1 +x_2\)로 유일하게 표현된다
단 (\(x_1 \in V\), \(x_2 \in V^\perp\))
ex)
v와 직교하는 다른 벡터 w에 대해 x가 있을 때,
x를 a벡터랑 b벡터로 분해하려면?
\(\Rightarrow\)
a = v에 평행한 a벡터 aka 부분벡터공간 v에 속한 벡터
b = w라는 v에 직교하는 여공간 속에 포함되는 b벡터
1. 행렬
1-1. 평면백터
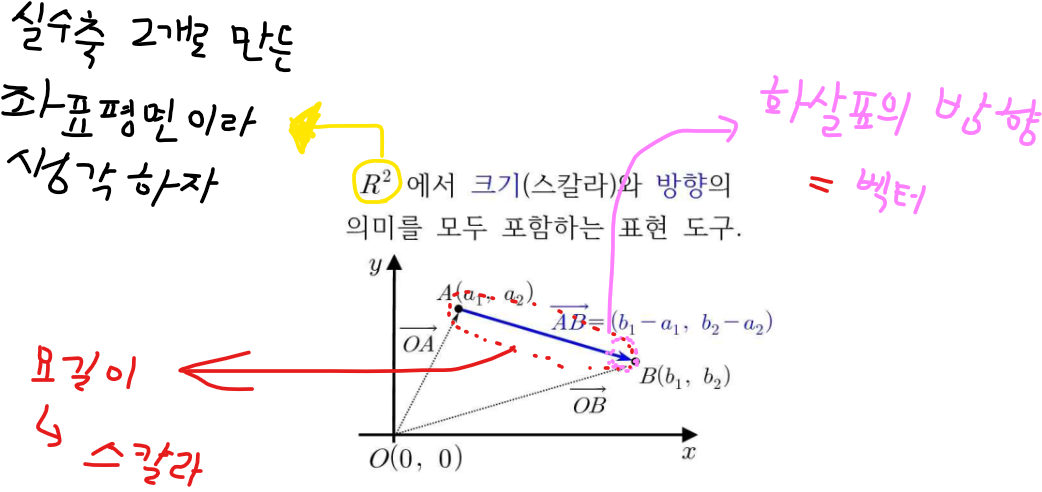
\(R^2\)에서 크기(스칼라)와 방향의 의미를 모두 포함하는 표현도구
(\(R^2\) —> 실수축 2개로 만들어진 좌표평면이라 생각해봅시다)
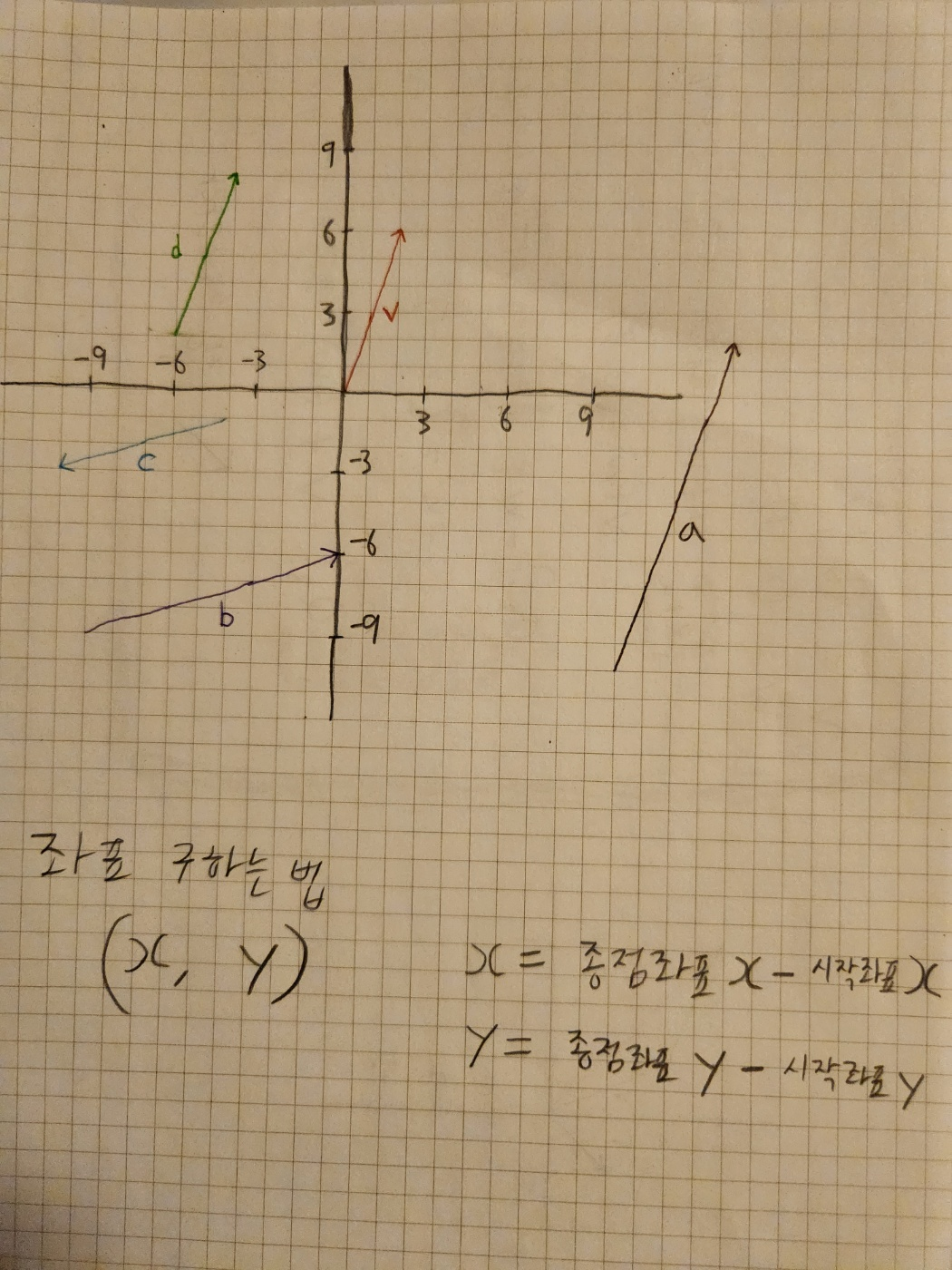
ex) 속도 = 벡터
속력 = 스칼라
벡터 v와 방향이 같은 벡터: a, d
벡터 v와 크기가 같은 벡터: c, d
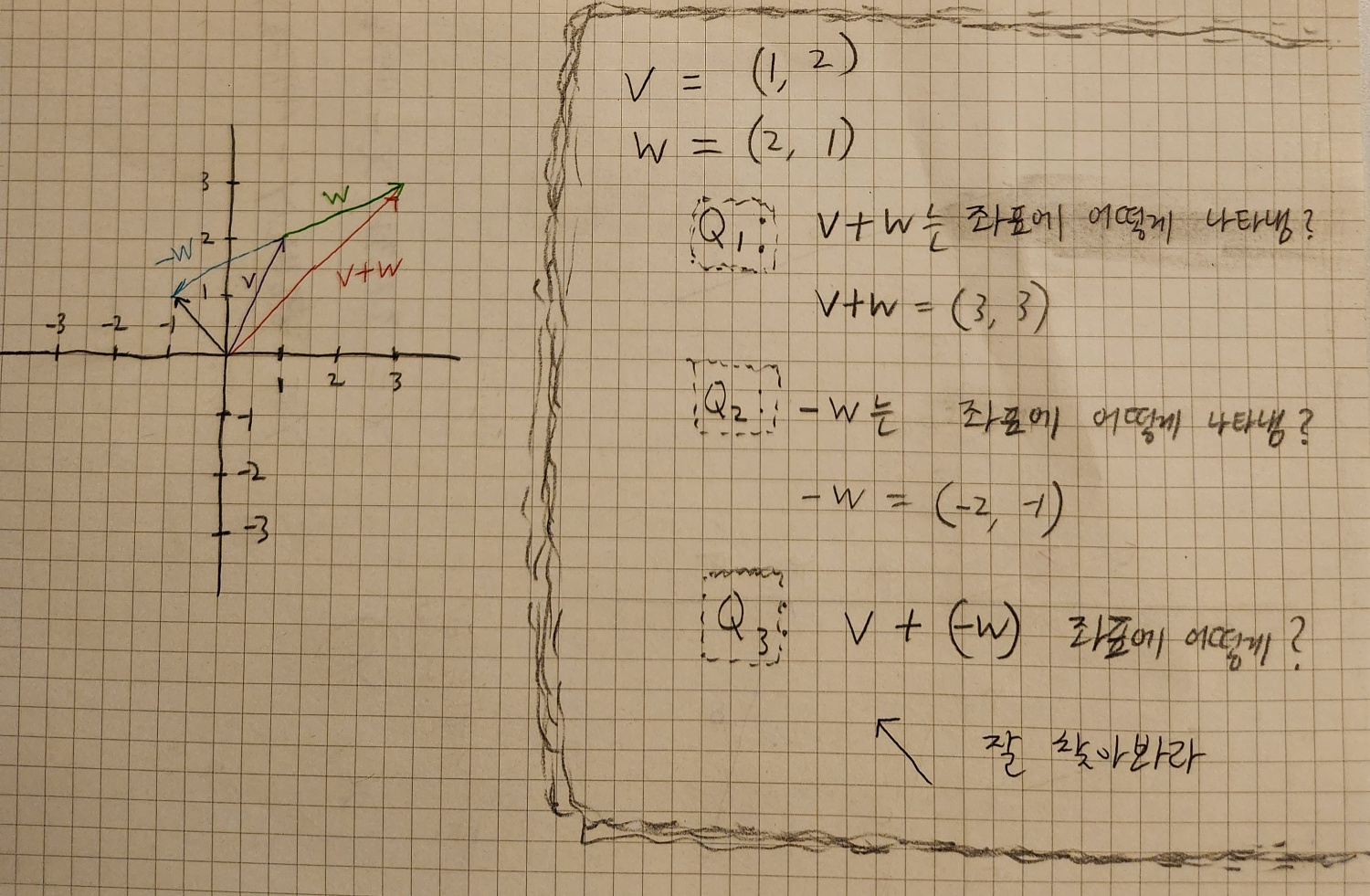
ex) v 벡터를 보자
(2-0, 6-0) 즉 2,6
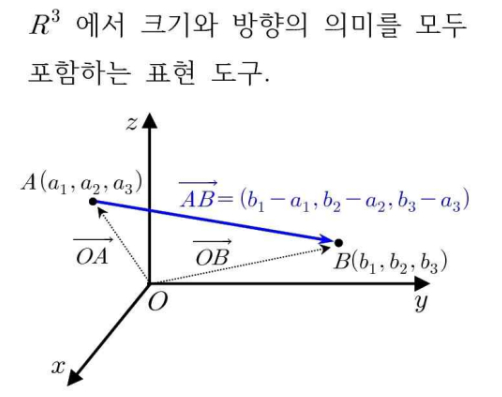
1-2. 공간벡터
1-3. n차원 벡터
2. 벡터의 연산
2-1. Norm
2-2. 선형결합
2-3. 스칼라 곱 + cosine simmilarity
cosine simmilarity
\(cos\theta=\frac{a \cdot b}{\vert a \vert \cdot \vert b \vert} = \frac{\sum\limits_{i=1}^N a_i b_i}{\sqrt{\sum\limits_{i=1}^N a_i^2}\sqrt{\sum\limits_{i=1}^N b_i^2}}\)
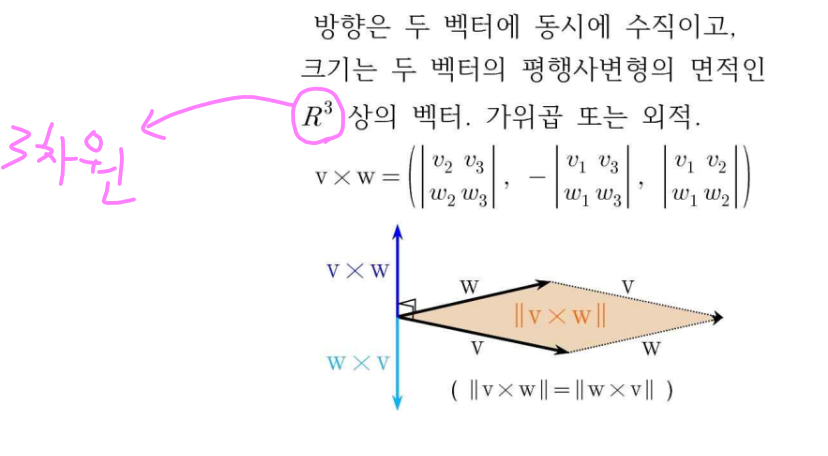
2-4. 벡터곱
3. 벡터의 응용
3-1. 직선의 표
3-2. 평면의 표현
4. 행벡터와 벡터내적간의 연관성
질문: 벡터의 내적이 기하학적으로 한 벡터에서 다른 벡터로의 정사영과 관련이 있을까?
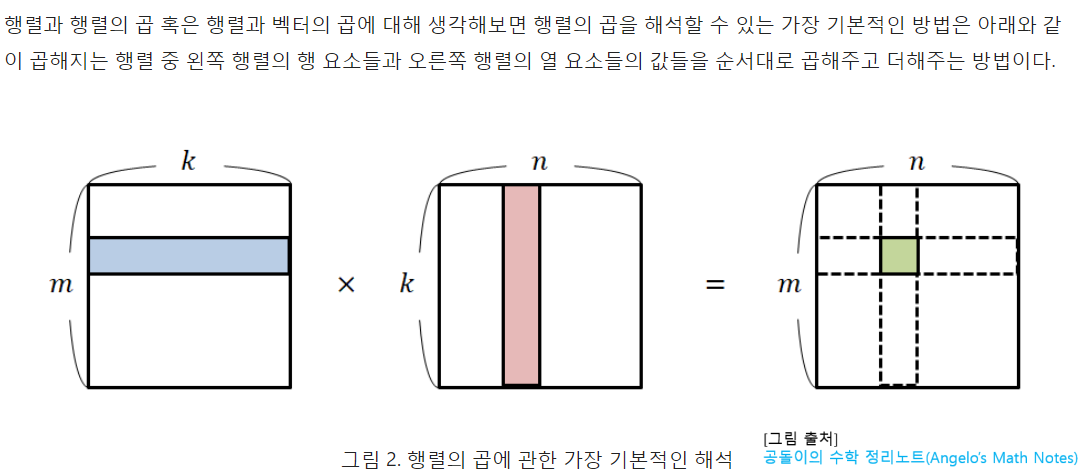관례적으로 변화가 되는 대상인 열벡터를 우리가 “흔히 말하는” 벡터라고 본다.
행벡터는 열벡터에 대한 함수로, 열벡터는 ‘변화의 대상’이 되는 것에 반해 행벡터는 변화를 시키는 행위자인 것이다.
가령 [2, 1]이라는 행벡터와 \([3, -4]^T\)라는 열 벡터에 대해 다음과 같은 곱셈을 생각해보자
\(\begin{bmatrix} 2 & 1 \end{bmatrix} \begin{bmatrix} 3 \\ -4 \end{bmatrix} = 2 * 3 + 1(-4) = 2\)
즉, 행벡터는 열벡터를 입력으로 받아 스칼라를 출력하는 \(f: V \Rightarrow R\) 인 함수
우선 ax+by+c = 0 인 식을 통해, 출력 스칼라 값4가 어떤 의미일지 확인하자
우리는 행벡터에 해당하는 [2, 1] 을 그리고 2x+y=4 라는 점까지의 거리를 생각하자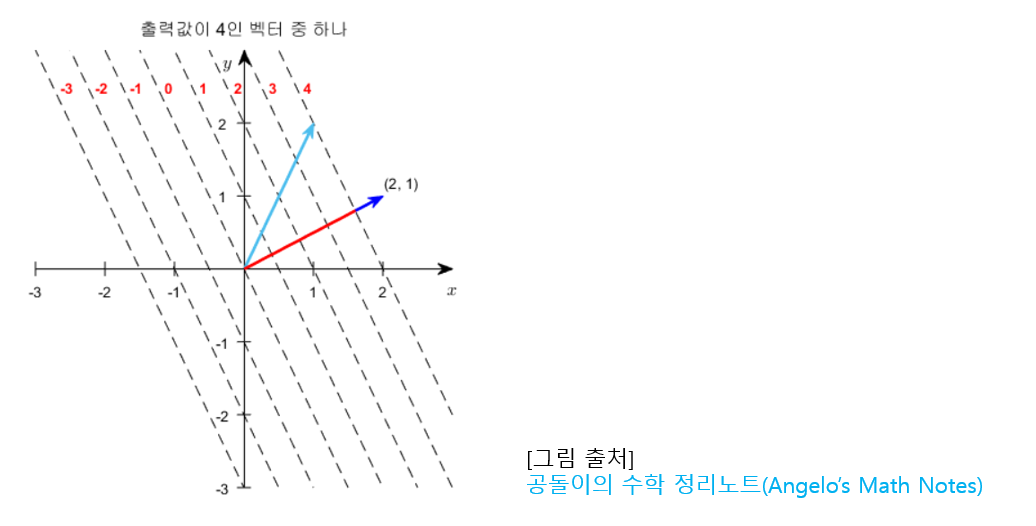 
생각해보면 2x+y=c에 해당하는 점선은 모두 행벡터 [2, 1]에 수직이다
why? –> 행벡터가 점선으로 표현한 함수들에 대해 법선 벡터역할을 하기 때문
따라서 위의 그림에서 빨간색으로 표현한 길이는 다음과 같이 직각 삼각형의 높이를 계산함으로써 얻을 수 있다.
직각 삼각형의 넓이를 구하는 방법을 이용해 d의 길이를 계산할 수 있다.
즉 4x2 = d * \(\sqrt 20\) 이므로, \(d=\frac{8}{\sqrt20} = \frac{4}{\sqrt5}\)이다
여기서 행벡터 [2, 1]의 길이는 \(\sqrt5\)인데, 이 길이를 d에 곱하면
\(d*\sqrt5 = \frac{4}{\sqrt5}*\sqrt5 = 4\)
즉 열벡터의 정사영 길이 * 행벡터의 길이 = 내적 값
결과값은 아래와도 똑같이 4로 같다
\(||v|| * ||w|| * cos60\)
이것은 다시 말해 열벡터의 정사영 길이가 내적 계산에 이용되기 때문임을 기하학적으로 확인할 수 있는 것이다.
5. 예제
5-1. cos theta
5-2. 두 벡터를 활용한 평행사변형 넓이
5-3. 직선과 평면이 동시에 만나는 좌표
6. 참고
[공돌이의 수학정리노트 (Angelo’s Math Notes)] 행벡터의 의미와 벡터의 내적
