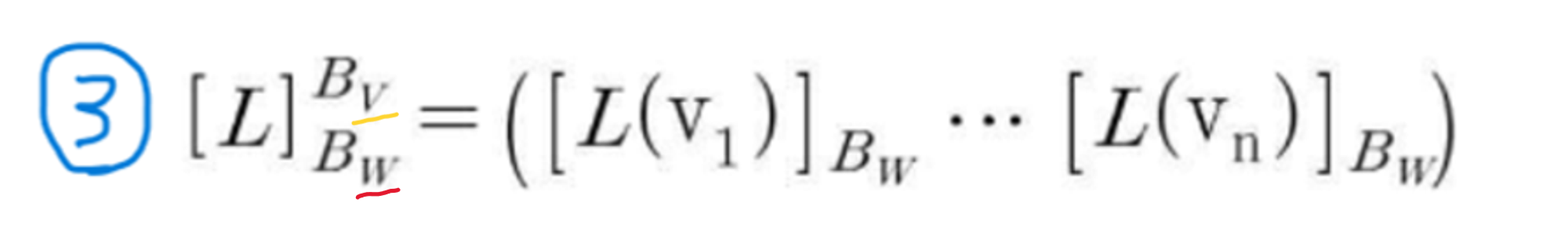[선형대수학] 4강. 선형사상
🙅♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
<목차>
* 참고
1. 선형사상
1-1 선형사상
1-2 여러 선형사상
2. 선형대수학의 기본정리
3. 차원정리
3-1 차원정리
3-2 비둘기집 원리
(1) 따름정리
(2) 비둘기집 원리
*만약 비둘기집에 선형대수학 논리를 적용시키려면?
4. 예제 (3개)
4-1 선형사상 증명
4-2 동형사상 증명
4-3 선형사상
*참고
1
2
3
4
5
6
7
8
9
10
------------------- ∈ vs ⊂ ------------------------------
∈ Element
A={1,2,3} 이면
2 ∈ A
2는 A의 원소이다.
⊂ 부분집합
A={1,2,3} B={1,3}일 때
B ⊂ A 이면 집합 B는 A의 부분집합이다.
1. 선형사상
1-1 선형사상
잠깐! 사상은 간단하게 얘기하자면, 대수구조를 다루는 함수
선형사상(L):
가산성 + 동차 라는 2개 공리(조건)를 동시에 만족하는 사상 
\(\text{가산성(Additivity):}\quad\quad L(u+v) = L(u) + L(v)\quad (u,\quad v \in V)\) \(\text{동차성(Homogeneity):}\quad\quad L(kv) = kL(v)\quad (k \in F,\quad v \in V)\)
u, v는 정의역에 해당하는 대수구조인 V(벡터공간)의 원소들입니다.
가산성에 대해 먼저 봅시다.
즉 L(u+v)는 내부에서 두 원소를 덧셈한 선형사상을 뜻하며 이는 결과인 L(u) + L(v)와 같습니다.
동차성에 대해 봅시다.
k라는 스칼라가 v에 곱해졌는데, 그걸 괄호 밖에 내도 똑같습니다.
>설명
- 핵(kerL)
선형사상의 결과가 0벡터가 되며, V(벡터공간)에 속한 v들을 모은 집합으로커널L이라고도 합니다. - 상
치역처럼 생각하면 되고, 선형사상의 결과들을 모두 모은 집합으로이미지L(imL)이라 합니다 자기사상
V라는 벡터공간과 W라는 벡터공간은 기본적으로 틀린데, 같을 때가 있습니다!
즉 정의역에 해당하는 V와 공역에 해당하는 W의 벡터들 같을 때입니다.
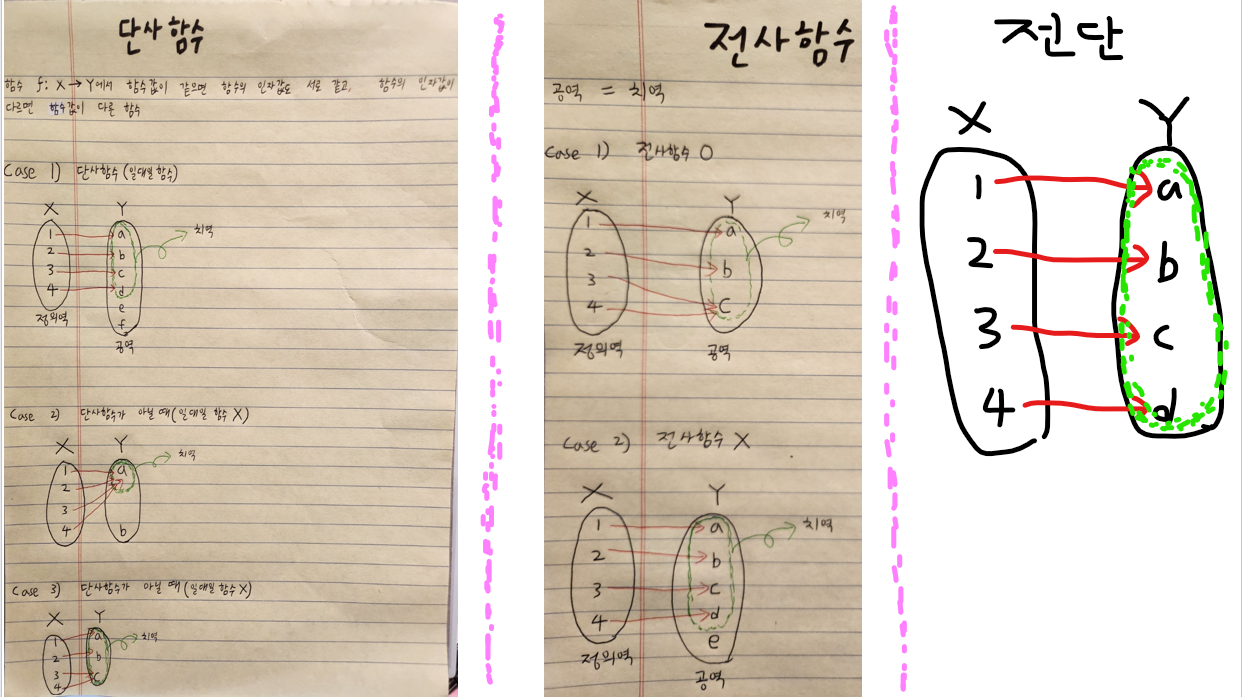
그럴 때, 선형사상을자기사상이라고 합니다.단사사상
V -> W 이걸 참고하여
V에서 서로 다른 2개의 벡터 v1, v2를 잡아줬을 때, 그에 대응되는 W의 벡터들도 서로 달라야 합니다
근데! L(u) = L(v)라면 벡터들인 u=v도 만족하는데 그걸단사사상이라 합니다!전사사상
V에 있는 벡터들이 전부다 W벡터들에 대응된 것
쉽게 표현하면 공역 = 치역
맨 위에*참고볼 것동형사상
단사사상도 되고 전사사상도 됨 aka 전단사
즉 동일한 대수구조를 판별함에 있어서 핵심이 됩니다자기동형사상
정의역과 공역이 같고, 동시에 1:1 대응인 사상사상의 합성
합성함수를 생각하면 편합니다
예시: g(x) = \(x^2\), f(x) = 2x \(h(x)=g(f(x))=(2x)^2 =4x^2\)- 역사상
역원이랑 비슷한 개념입니다
L2 * L1 = Iv로 항등사상 나왔을 때,
L2와 L1 위치 바꿨을 때도 항등사상이면 그때 비로소 역사상이 됩니다
2. 선형대수학의 기본 정리
F-벡터공간 V, W에 대해 V → W로의 선형사상들의 집합을 L(V, W)라 하고,
다음과 같이 L(V, W) 위의 합과 스칼라배를 정의한다
조건 = \((v \in V, \quad k \in F) \\\)
1) 합 = \((L_1 + L_2)(v)\) = \(L_1(v) + L_2(v)\)
2) 스칼라배 = \((kL)(v)\) = \(kL(v)\)
F에 속한 m x n 행렬들의 집합을 아래와 같이 나타냅니다 \(M_{m*n}(F)\)
두 사상 \(f\), \(g\)는 다음과 같이 정의합니다
\(f: \quad L(V, W) \rightarrow M_{m*n}(F) \\ 정의방법: \quad f(L) = [L]_{Bw}^{Bv} = M \\[5ex] g: \quad M_{m*n}(F) \rightarrow L(V, W) \\ 정의방법: \quad g(M) = L_M([L_M(v)]_{Bw} = M[v]_{Bv}\)
[기호 참고]
1
2
3
4
-->: 가는 방향
사상f: 선형사상 --> 행렬집합의 대수구조
사상g: 행렬집합의 대수구조 --> 선형사상
1번 설명
ex-1): V = \(|R^3\)$ \color{red}{\Rightarrow} $\(B_v\)= {(1,0,0),(0,1,0),(0,0,1)}
위는 예를 든 수식입니다
이는 벡터공간 V가 3개의 기저벡터로 구성된 것을 나타냅니다
v1, v2, v3을 각각 (1, 0, 0), (0, 1, 0), (0, 0, 1)로 임의 설정했을 때 그 배치순서는 고정합니다.
이것으로 Bv = V의 순서기저가 됩니다.
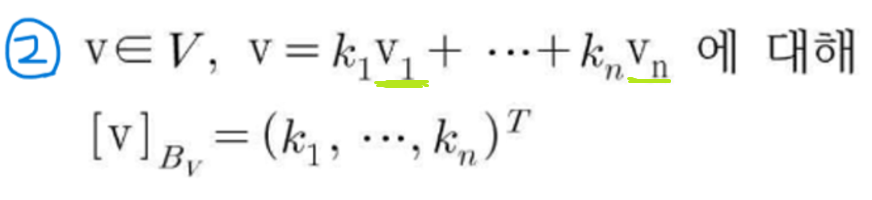V에 속한 v를 갖고와서 \(v_1\) ~ \(v_n\)까지 벡터들이 Linear combination(선형결합)을 했을 때,
\(k_1\) ~ \(k_n\)까지 모은 튜플을 행에서 열로 전치시켰네요
\(B_v\)는 꼭 표준기저일 필요는 없는데 여기서 \(B_v\)는 \(v_1\) ~ \(v_n\)까지를 나타냅니다
2번 설명
1번 v1, v2, v3에 이어서 합니다
ex-2): \(v \in V, \quad v = 3V_1 + V_2 + 2V_3 \\[3ex]\) $ \color{red}{\Rightarrow} $ m\((3, 1,2)^T\) $ \color{red}{\Rightarrow} $\(즉\begin{bmatrix} 3\\ 1 \\ 2 \end{bmatrix} 이는 \quad [v]_{Bv}다\)
기저는 아까 언급했듯이 어떤 것이든 상관없는데, 어떤 기저를 잡으면 그 기저에 대해 v라는 벡터를 \(3V_1 + V_2 + 2V_3\) 처럼 표현하겠다는 뜻입니다.
왜 \(3v_1,v_2,2v_3\)이 아니고 대문자인 \(3V_1, V_2, 2V_3\)이냐?
$ \color{blue}{\Rightarrow} $ 기저벡터는 보통 대문자, 특정벡터는 소문자입니다
\(B_v \Rightarrow B_w\)
1
2
3
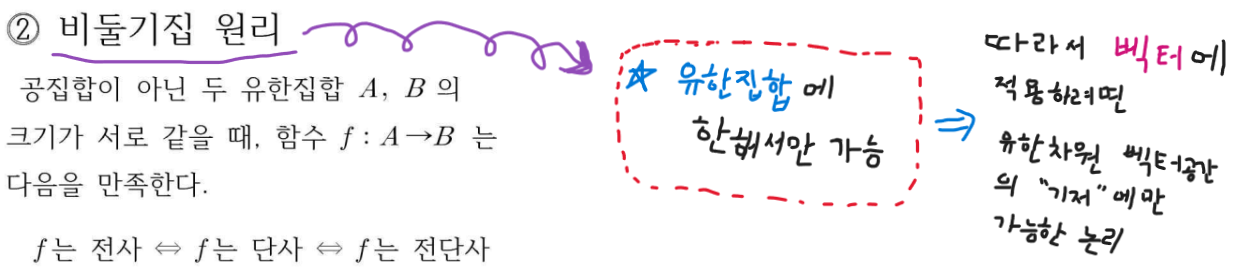
v1: V의 원소
L(v1): 선형변환을 거친v1 즉 L(v1)는 w의 원소
--> 즉 L(v1)을 분리시키려면 w기저를 따라야 한다.
3번 설명
3. 차원정리
잠깐! 커널의 개념 다시 한번 짚고 들어가겠습니다.
선형사상 \(L: IR^n \rightarrow IR^m, \quad L(x) = \vec{0}\) 를 만족하는 모든 x들의 집합
3-1 차원정리
L: V -> W 에 대하여 다음이 성립한다
dim($ \color{red}V$) = dim(ker $\color{lightblue}L $) + dim(im $\color{lightblue}L $)
요약본과 A to Z 방식으로 총 2개 작성합니다.
요약본
A to Z
3-2 비둘기집 정리
—> n+1개의 물건을 n개의 상자에 넣을 때 적어도 어느 한 상자에는 두 개 이상의 물건이 들어 있다는 원리
*만약 비둘기집에 선형대수학 논리를 적용시키려면?
조건 임의설정: L이 V에서 W로 가는 선형사상
-> 그러면 L(v)에서 가능한 v의 선택지는 1차원이라도 무한개
L(v), L(2v)이런식으로 모든 v에 대해서 다 함수값을 정해줘야 하는데,
귀찮기에 유한개로 정의하고 끝내자
(우선 L(v)를 f(x)로 생각하면 편하다)
기저 { \(v_1\) , \(...\) , \(v_n\) } 에서 L의 함수값을 정하면
\(L(v)\) = \(L(a_1v_1 + ... + a_nv_n)\) = \(a_1L(v_1) + ... + a_nL(v_n)\) 이라서
모든 함수의 벡터값이 다 정의된다
4. 예제 (3개)
4-1 선형사상 증명
1
*이 문제를 풀기 위해서는 가산성, 동차성을 증명해야한다
4-2 동형사상 증명
1
2
3
* 3차 다항식 집 --> 4차원
L1과 L2가 동형사상이 되기위한 산식을 증명해봐라
즉, 한 대수구조에서 다른 대수구조로 가는 사상의 구체적인 산식을 알맞게 정의하라는 뜻
4-3 선형사상
