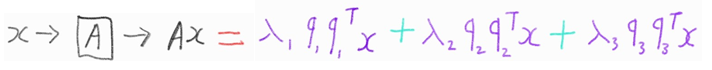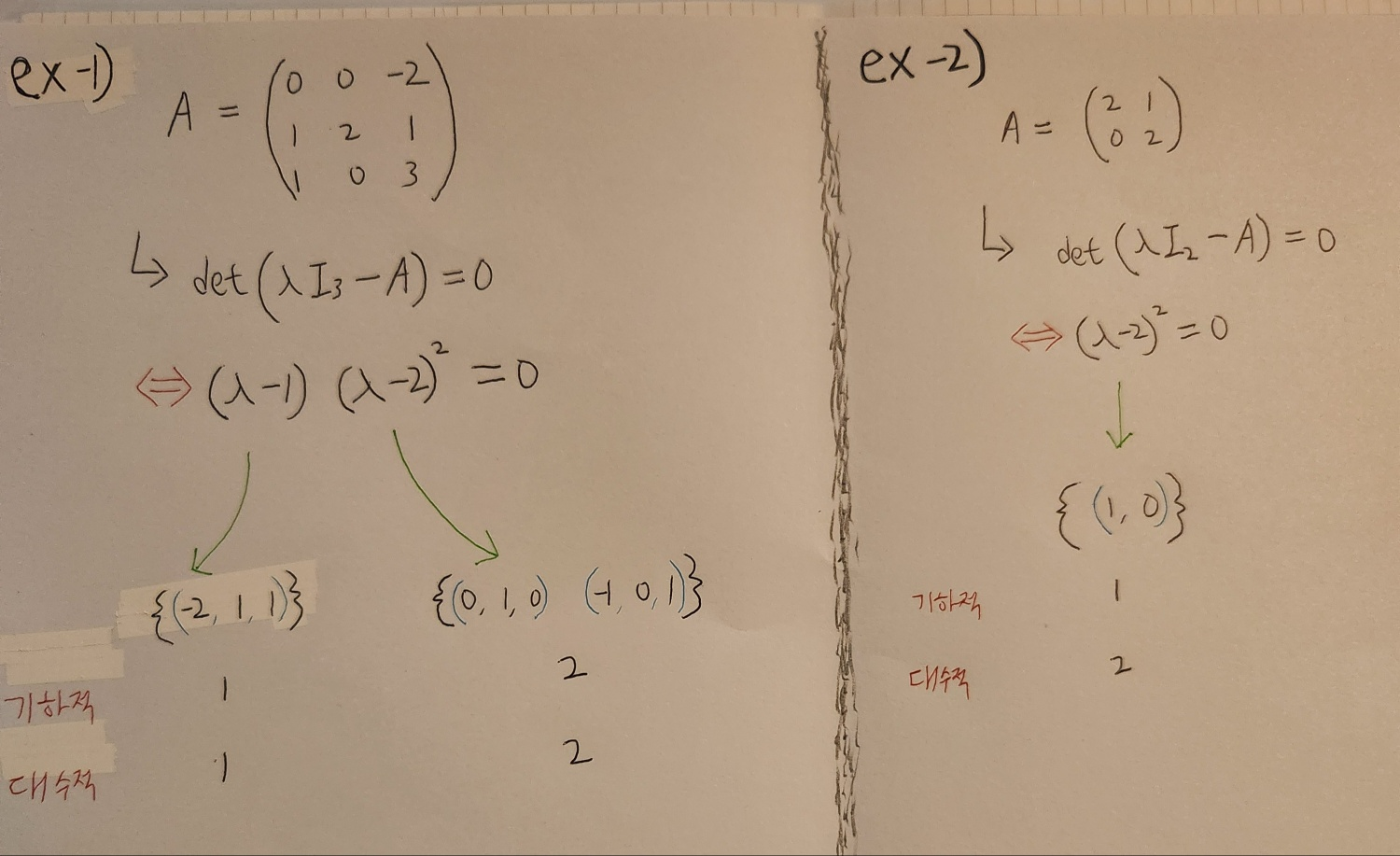Eigen Decomposition

🙅‍♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다

0. 들어가며

1. Eigen decomposition (long provement)
 1-1. Eigen decomposition to diagonalization
 1-2. Eigen decomposition 장점(5개) & 꿀팁(3개)

2. feature of symmetric matrix
 2-1. 표현
 2-2. 실생활 응용
 2-3. 새로운 해석  

3. 대각화 판별법
 ★대각화 가능, 불가능 사례
 3-1 중복도  
 3-2 닮음 불변량

4. 케일리-해밀턴 정리

5. 연습문제 (3개) 고유값,고유벡터 2개, 케일리해밀턴 1개

0. 들어가며

우선 요약본인데 잠시 훑어보고 지나가는 것도 나쁘진 않을 것 같습니다.
EVD 즉 고윳값 분해를 위한 식은 아래와 같이 나타낼 수 있습니다.
행렬Ax가 있을 때
$Ax = \lambda_1q_1q_1^Tx+\lambda_2q_2q_2^Tx+\cdots+\lambda_nq_nq_n^Tx$

여기서 dim reduction을 하여 고유벡터 2개만 사용할시
$Ax \approx \lambda_1q_1q_1^Tx+\lambda_2q_2q_2^Tx$ 아무튼 서론이 좀 길었는데 거두절미하고,

이번 글에서의 주요 내용인 행렬을 고윳값과 고유벡터로 분해하는 과정인 Eigenvalue Decomposition(고윳값 분해)에 대한 내용과, symmetric matrix의 실생활 응용 및 새로운 해석에 관해 알아볼 것입니다

1. Eigen decomposition (long provement)

——————— 뜻 ———————-
characteristic equation(고유방정식)
$det(\gamma I_n - M)$ $\Rightarrow$ 고유값, 고유벡터를 찾는 과정

diagonalization
$A=V\gamma V^{-1}$
——————————————-

1-1. Eigen decomposition to diagonalization

$A_{2*2}$ 가 있다고 하자 이때
eigen value (2개)   $\gamma_1, \gamma_2$
eigen vector(무조건 independant) 2개   $v_1,~ v_2$

그러면 자연스럽게 $Av_1=\gamma_1v_1$,       $Av_2=\gamma_2v_2$ 가 된다
여기서 2개의 수식을 하나로 합쳐보자
$A\left[v_1, ~~~ v_2\right] = \left[\gamma_1 v_1, ~~~ \gamma_2 v_2\right]$

오 이식을 이렇게 바꿀 수도 있군
$=\begin{bmatrix} v_1, ~~ v_2 \end{bmatrix} \begin{bmatrix} \gamma_1 & 0 \\ 0 & \gamma_2 \end{bmatrix}$

자 이식에서 $\begin{bmatrix} v_1, ~~~ v_2 \end{bmatrix}$는 v만 모아놓은 것이니 행렬V라 하자
$V=\begin{bmatrix} v_1, ~~~ v_2 \end{bmatrix}$, 마찬가지로 $\gamma=\begin{bmatrix} \gamma_1 & 0 \\ 0 & \gamma_2 \end{bmatrix}$
어 그러면 식을 이렇게도 바꿀 수 있겠다 $\Rightarrow AV = V\gamma$

그럴 때, $v_1, ~~~ v_2$는 independant한 vector로 삼으니 그럼 이건 원래 rank가 2 by 2인 행렬인데도 2개다
즉 invertable하다   why? ($det \neq 0$ 이니까 역행렬 존재해서)

그래서 이렇게 식을 바꿀 수 있다 $\Rightarrow A=V\gamma V^{-1}$
🤔만약에 여기서 식을 이렇게 바꾸면? $\Rightarrow V^{-1}AV=\gamma$
당연히! $\gamma$는 diagonal matrix니까 eigen decomposition이 되는 A를 “diagonalizable하다”라고 한다

다시 말해
$A_{n*n} \Rightarrow diagonalizable$ $\color{red}{\Leftrightarrow}$ independant Eigen vector가 n개다
——————— 뜻 ———————-
n by n의 A행렬이 diagonalizable하면 independant Eigen vector가 n개라는 것과 동치다
——————————————-

1-2. Eigen decomposition 장점(5개) & 꿀팁(3개)

🤵‍♀️장점

(1) $A^k$    ex) $A^3=V\gamma V^{-1}$ $\color{red}{\cdot}$ $V^{-1}\gamma V$ $\color{red}{\cdot}$ $V\gamma V^{-1}$ $\color{red}{=}$ $V\gamma^{3} V^{-1}$

----------------sol-(1)-------------------
$\gamma^k는 \quad \begin{bmatrix} \gamma^k & 0 \\ 0 & \gamma^k \end{bmatrix}$   인데 제곱, 세제곱, 네제곱…은 $\gamma$ 값만 바꿔주면 되어 계산이 편하다
-------------------------------------------

(2) $A^{-1} \color{red}{=}$ $\left(V\gamma V^{-1}\right)^{-1} = V \gamma^{-1}V^{-1}$

----------------sol-(2)-------------------
$\begin{bmatrix} \gamma_1 & 0 \\ 0 & \gamma_2 \end{bmatrix}^{-1} = \begin{bmatrix} \frac{1}{\gamma_1} & 0 \\ 0 & \frac{1}{\gamma_2} \end{bmatrix}$
자 여기서 $A^{-1}A$ 확인하자 $\color{red}{\Rightarrow}$ $V \gamma^{-1}V^{-1}$ $\color{red}{\cdot}$ $V\gamma V^{-1}$ 하면 바로 항등행렬I가 되네
마찬가지로 위치를 바꿔 $AA^{-1}$ 해도 항등행렬I 나옴
-------------------------------------------

(3) $det(A)\color{red}{=}$ $det\left(V\gamma V^{-1}\right) = det(V) det(\gamma)det(V^{-1}) \\ \quad \Rightarrow det(\gamma) = \gamma_1 \color{red}{\cdot} \gamma_2 \cdots = \prod_{i=1}^{n} \gamma_i$

(4) $tr(A) = \left(V\gamma V^{-1}\right)$

----------------sol-(4)-------------------
참고:
trace: 정방행렬의 대각성분의 합 ex)   $A=\begin{bmatrix} 1 & 0 \\ 0 & 4 \end{bmatrix} \quad\quad tr(A)=1+4=5$
그리고 tr(ABC)= tr(BCA)=tr(CBA)
자 이게 위치를 바꿔도 같다는 성질을 이용하여

$tr\left(V\gamma V^{-1}\right)=tr\left(\gamma V^{-1}V\right) = tr\left(\gamma \right)$
$\Rightarrow \gamma_1 \color{red}{+} \gamma_2 \color{red}{+} \cdots \quad\quad\quad \color{violet}{\therefore} \sum\limits_{i=1}^n\gamma_i$
-------------------------------------------

(5) rank-difficient $\color{red}{\Leftrightarrow} det(A)=0 \color{red}{\Leftrightarrow} 0$ 인 eigen value가 1개 이상 존재

----------------해석-(5)-------------------
rank-dificient는 det=0인 것과 동치인데 det는 $\gamma$ 를 싹 곱한 것이니 그말은 즉슨
0인 eigen value가 1개 이상 존재한다는 뜻
-------------------------------------------

🍯꿀팁

(1) $A^T$의 Eigen value $\color{red}{=}$ A의 Eigen value

----------------sol-(1)-------------------
why? $\Rightarrow det(A-\gamma I) = det(A-\gamma I)^{T}$
왜냐하면 $det(A) = det(A)^T$ 라서
$\therefore det(A-\gamma I) = det(A^T-\gamma I)$
-------------------------------------------

(2) A가 orghogonal matrix면   $\gamma_i = \pm 1$ 이다

----------------sol-(2)-------------------
우선 orthogonal matrix를 Q로 두자 빨빨빨빨강, 그리고 거기에 행렬 v를 통과시키자
$QV=\gamma V$
$\left(Qv\right)^{T}Qv= V^TQ^TQV=V^TV= \parallel V \parallel_2^2$
어?   여기서 $\left(\gamma V\right)^{T}\gamma V$ 이렇게 고칠 수도 있는데    그러면 $\color{red}{\therefore} \gamma^2\parallel V \parallel_2^2$
-------------------------------------------

(3) A가 positive semi-difinite(P.S.D)면 $\color{red}{\Leftrightarrow} \quad \gamma_i \ge 0$

----------------sol-(3)-------------------
(이때 $A= A^T\color{red}{,} \quad$ 즉 symmetric matrix)

그나저나 PSD??? ⬇️
$z^TAz \ge 0$ 이고 이것은 z를 선형변환한 것인데 z와 내적했을 때 양수가 된다는 것은
선형변환을 거쳐도 직교하는 평면 뒤쪽으로 안튀어나간다는 말이다
(즉 어떤 벡터를 통과시키더라도 아래 그림처럼만 바뀐다)

내적했을 때 음수가 되는 $90^{\circ}$ 방향을 넘어가지 않는다

이어서 식을 바꿔보자
$Az=\gamma z$ 로 두면 $z^T \gamma z \ge 0$ 된다 $\color{red}{\Rightarrow} \quad \vert\vert z\vert\vert_2^2 \gamma\ge 0$
$\color{red}{\therefore}$ 자 $\vert\vert z\vert\vert_2^2$가 양수니 $\gamma$도 무조건 양수이게 된다
-------------------------------------------

(4) ⭐(핵중요) Diagonalizable matrix A의 non-zero eigen value의 수 = rank(A)

----------------sol-(4)-------------------
----------------참고:-----------------
(diagonalizable Matrix 라고 반드시 symmetric은 아니다)
-----------------------------------
$A = V \gamma V^{-1} = rank(\gamma)$

case 1):
$\begin{bmatrix} \gamma_1 & & \\ & \gamma_2 & \\ && 0\end{bmatrix}$
이것은 0이 있으니 막혀서 rank2

case 2):
$\begin{bmatrix} \gamma_1 && \\ & \gamma_2 & \\ && \gamma_3 \\ &&& \ddots \end{bmatrix}$
0이 나오기 전까지 rank 계속 갯수 셈
-------------------------------------------

2. feature of symmetric matrix

2-1. 표현

if $A=A^T$    then, symmetric matrix is diagonalizable

--------------------sol----------------------
$A = V \gamma V^{-1}$
$A^T = V^{-T}\gamma V^{T}$ 이 된다. 그럼 자연스럽게 $V=V^{-T}\color{red}{,} \quad\quad V^{-1}=V^T$ 으로
만족하도록(orthogonal matrix 이도록) V를 설정할 수 있다

여기까지 확인했으면 orthogonal Matrix는 보통 Q로 표기하니 다시 $A=Q\gamma Q^T$ 로 바꿔적자
💡즉 symmetric matrix는 diagonalizable하며 $A=Q\gamma Q^T$ 가 된다
----------------------------------------------

2-2. 실생활 응용

Q가 가지는 컬럼을 통해 $Q\gamma Q^T$를 표현해보자

(Q는 3x1,   $Q^T$ 는 1x3이다)

$A=\begin{bmatrix} q_1 & q_2 & q_3 \end{bmatrix} \begin{bmatrix} \gamma_1 & & \\ & \gamma_2 & \\ && \gamma_3\end{bmatrix} \begin{bmatrix} q_1^T \\ q_2^T \\ q_3^T\end{bmatrix}$

어? $q_1 \perp q_1^T\color{red}{,} \quad q_2 \perp q_2^T\color{red}{,} \quad q_3 \perp q_3^T$로군

$=\begin{bmatrix} \gamma_1q_1 & \gamma_1q_2 & \gamma_1q_3 \end{bmatrix} \begin{bmatrix} q_1^T \\ q_2^T \\ q_3^T \end{bmatrix} \\ \Rightarrow \gamma_1q_1q_1^T+\gamma_2q_2q_2^T+\gamma_3q_3q_3^T$
오! 이거 $q_1q_1^T$ 는 자연스럽게 Rank1 Matrix니까 행렬은 slice로 쪼갠거네

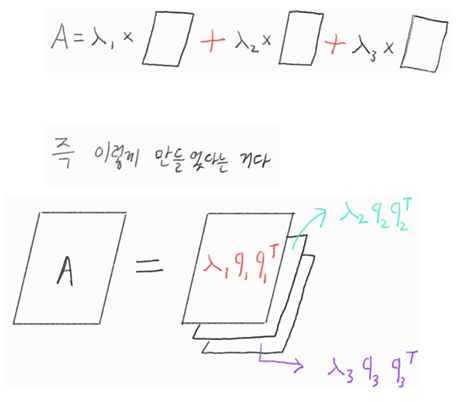
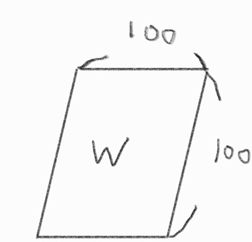
아 이거 100퍼 데이터 압축에 응용가능하다

ex) 사진 W가 100x100 이라 하면 10000개의 숫자가 필요하다.

이걸 쪼개서 5개만 쓰자 $\gamma_1q_1q_1^T+\gamma_2q_2q_2^T+ \cdots \gamma_{10000}q_{10000}q_{10000}^T$

그럼 $\gamma$에 대해 5개가 필요하고 q가 100x1이니까 총 5개 있어서 500
그래서 합하면 505개다
$\color{red}{\therefore}$ 즉 10000개 중에서 505개를 쓴다는 건데 선명하지 않고 화질이 매우 구리지만 인식은 될 것이다

2-3. 새로운 해석

--------------------cond(조건)----------------------
$A=A^T$면 $A=\gamma_1q_1q_1^T+\gamma_2q_2q_2^T+\gamma_3q_3q_3^T$
(A: 3x3행렬이고,    $q_1 \perp q_2 \perp q_3$)
---------------------------------------------------------

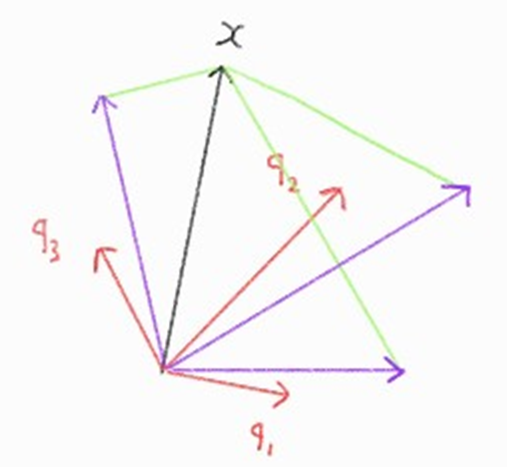
여기서 x라는 Eigen vector가 아닌 임의의 벡터를 행렬A에 통과시켜 decompose한 상태로 들여보자

어? $q_1^Tx \quad\quad q_2^Tx \quad\quad q_3^Tx$ 는 각각 x랑 내적한거네??
그러면 $q_1 \quad\quad q_2 \quad\quad q_3$ 는 각각 방향벡터다
그렇다면 $q_1q_1^Tx \quad\quad q_2q_2^Tx \quad\quad q_3q_3^Tx$ 는 각각 projection이네 ??

🏜️그림 예시

x라는 벡터가 있을 때 직교하는 $q_1 \quad\quad q_2 \quad\quad q_3$가 있다 하자
$\color{lightgreen}{/}$선들을 아래로 내리면 $\color{purple}{\nearrow}벡터$들이 대응될 것이다

3. 대각화 판별법

판별법을 보기전 우선 대각화 불가능사례와 가능한 사례를 먼저 보고자 한다

예시 ㄱ) 대각화 불가능 사례

$A = \begin{pmatrix} 2 & 1 \\ 0 & 2 \end{pmatrix}$   는 대각화 가능한가?

*위의 행렬 A가 대각화가 가능하려면 선형독립인 고유벡터가 2개가 나와야함

1️⃣고윳값 구하기

고유방정식 $\color{red}{\Rightarrow}$ $det(\gamma I_2 - A)= det \begin{pmatrix} \gamma-2 & -1 \\ 0 & \gamma-2 \end{pmatrix} = (\gamma-2)^2 = 0 \\ \Leftrightarrow \gamma =2(중근)$

2️⃣고유벡터 구하기

$(2I_2 - A)v = 0 \\ \Leftrightarrow \begin{pmatrix} 0 & -1 \\ 0 & 0 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}$

여기서 v는 free variables인 s 하나 잡고 (1,0)을 하던 (-1,0)을 하던 상관없는데,
(1,0)으로 선택하겠습니다.

$\color{red}{\Rightarrow}$ 즉 $v = s\begin{pmatrix} 1 \\ 0 \end{pmatrix}$   으로 대각화 불가능
왜? —> 고유기저 = {(1,0)}   1개라서 안된다!
왜냐하면 선형독립인게 2개가 잡히려면 고유기저가 2개가 필요
(행렬의 n x n)에서 행 or 열갯수랑 매치될 것

예시 ㄴ) 대각화 가능 사례

아까 위의 내용을 토대로    $A = \begin{pmatrix} 1 & -2 \\ 3 & -4 \end{pmatrix}$   에 대한 P 찾기

이건 된다 왜냐하면 $\gamma(고윳값) =-1$   일 때,
$\rightarrow 고유벡터 (s,s)$
$\rightarrow P_1\begin{pmatrix} 1 \\ 1 \end{pmatrix}$   일 때, $\rightarrow 고유벡터 (2t,3t)$

$\gamma(고윳값) = -2$   일 때
$\rightarrow P_2\begin{pmatrix} 2 \\ 3 \end{pmatrix}$

즉 $P = P_1 P_2 = \begin{pmatrix} 1 & 2 \\ 1 & 3 \end{pmatrix} \\ P^{-1} = \begin{pmatrix} 3 & -2 \\ -1 & 1 \end{pmatrix} \\ P^{-1} A P = B$

참!   $P_2 P_1$   로 위치를 바꿔 열벡터들을 나열하여 계산해도 대각화가 됩니다!

3-1 중복도

대각화가 가능한지 판별하는 또 다른 방법입니다
기하적 중복도, 대수적 중복도를 비교하여 구할 수 있습니다
일단 요약하면 기하적 중복도 = 대수적 중복도   일 때, 행렬의 대각화가 가능 합니다

기하적 중복도:
고유값에 대응하는 고유공간의 차원 갯수

대수적중복도:
고유 다항식에서 $\gamma-\gamma_0$ 가 인수로 나타나는 횟수
(대수적으로 고유값이 총 몇 거듭제곱인지?)

👉고유벡터, 고유기저를 잘 모르겠다면 이것 클릭

3-2 닮음 불변량

두 정사각행렬 A, B에 대하여 $B = P^{-1}AP$   를 만족하는 가역행렬 P가 존재하면
A, B는 서로 닮은 행렬이라 하고, 기호로 A~B라 표현한다.

서로 닮은 두 행렬의 다음과 같은 성질들은 서로 일치한다.
그 중에 일단 10개만 보겠습니다

(1) 행렬식
(2) 가역성 
(3) rank 
(4) nullity 
(5) 고유다항식(고유방정식의 좌변을 얘기함) 
(6) 고윳값 
(7) 고유공간의 차원 
(8) 대각성분들의 합 
(9) 대수적 중복도 
(10) 기하적 중복도 

서로 닮아 보이더라도, 선형사상들은 일반적으로 파악하기가 복잡한데
상당히 많은 선형사상들이 이 특성들 중 최소 한개라도 따를 확률이 높으니
선형사상들을 분해하여 간소화된 선형사상들에게서
저 특성들 중 최소 1개 이상을 찾을 수 있습니다
(즉 복잡하게 말고 쉽게쉽게 보자는 얘깁니다)

4. 케일리-해밀턴 정리

임의의 정사각행렬 A과 그 고유다항식
$f(\gamma) = det(\gamma I - A) = \sum\limits_{i=0}^n a_i\gamma^2$    에 대하여

$f(A) = 0$ 이 성립하며, 이를 캐일리-해밀턴 정리 라고 한다.    (단, 0은 영행렬)

쉽게 말하면 람다자리에 A행렬을 넣었더니 영행렬이 나오더라

이 글에서는 예시 2가지를 작성합니다

ex-1)

$A = \begin{pmatrix} 1 & -2 \\ 3 & -4 \end{pmatrix} \\ f(\gamma) = det(\gamma I_2 - A) \\ = det \begin{pmatrix} \gamma-1 & 2 \\ -3 & \gamma+4 \end{pmatrix}$

그러면 $\gamma$ (고유값)는 아래와 같이 나옵니다
$= \gamma^2 + 3\gamma + 2$

이걸 아래처럼 고칠 수도 있습니다
$= a_2\gamma^2 + a_1\gamma^1 + a_0\gamma^0$

여기서 A행렬을 대입하면 다음과 같습니다
$f(A) = A^2 + 3A + 2I = 0 \quad 성립하는가?$

$f(A) = \begin{pmatrix} 1 & -2 \\ 3 & -4 \end{pmatrix}^2 + 3\begin{pmatrix} 1 & -2 \\ 3 & -4 \end{pmatrix}^1 + 2\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \\ \\ \Leftrightarrow \begin{pmatrix} -5 & 6 \\ -9 & 10 \end{pmatrix} + \begin{pmatrix} 3 & -6 \\ 9 & -12 \end{pmatrix}+ \begin{pmatrix} 2 & 0 \\ 0 & 2 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} = 0$

ex-2)

행렬   $A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$ 에 대하여

$A^3$   를 케일리 해밀턴 정리를 이용해 A와 단위행렬 $I_2$ 로써 표현하시오.

풀이:

$A^3$ 를 이용하는 것보단,
$A^2$ 를 이용하는게 푸는데 더 쉬울 수도 있습니다.

$f(\gamma) = det(\gamma I_2 - A) = det \begin{pmatrix} \gamma-1 & -2 \\ -3 & \gamma-4 \end{pmatrix} = \gamma^2 -5\gamma-2 \\ \rightarrow f(A) = A^2 -5A -2I_2 =0 \quad 성립하는가?$

$\rightarrow f(A) = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} - 5\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} - 2\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} = 0$

이를 통해 $A^2 = 5A+2I$   라는 것을 확인할 수 있습니다
그러면 이어서 마저 계산해봅시다

$A^3 = 5A^2 + 2A \\ \Leftrightarrow A^3 = 5(5A + 2I_2) + 2I_2 \\ \Leftrightarrow A^3 = 27A + 12I_2$

5. 연습문제 (3개) 고유값,고유벡터 2개, 케일리해밀턴 1개

5-1 😀예제1

$M = \begin{pmatrix} 0 & 0 & -2 \\ 1 & 2 & 1 \\ 1 & 0 & 3\end{pmatrix}$   의 고윳값, 고유벡터 고유기저 구하기

step 1    고윳값 구하기
(고유방정식부터 구합시다.)

$det( \gamma I_3 - M) \\ \Leftrightarrow det\begin{pmatrix} \gamma & 0 & 2 \\ -1 & \gamma - 2 & -1 \\ -1 & 0 & \gamma -3 \end{pmatrix} \\ \Leftrightarrow det = \gamma \begin{vmatrix} \gamma-2 & -1 \\ 0 & \gamma-3 \\ \end{vmatrix} - 0 \begin{vmatrix} -1 & -1 \\ -1 & \gamma-3 \\ \end{vmatrix} + 2 \begin{vmatrix} -1 & \gamma-2 \\ -1 & 0 \\ \end{vmatrix} \\ \Leftrightarrow\gamma(\gamma^2-5\gamma+6) + 2(\gamma-2) = 0 \\ \Leftrightarrow(\gamma-1)(\gamma-2)^2 = 0$

즉 고유값:    $\gamma$ = 1 or 2

step 2고유벡터 구하기

case 1) $\gamma = 1$

$$(\gamma I_3 - M)v = 0 \\ \Leftrightarrow \begin{pmatrix} 1 & 0 & 2 \\ -1 & -1 & -1 \\ -1 & 0 & -2 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ v_3\end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$$

$\Leftrightarrow \begin{pmatrix} 1 & 0 & 2 & 0\\ -1 & -1 & -1 & 0\\ -1 & 0 & -2 & 0\end{pmatrix}$ $\color{red}{\Rightarrow}$ $\begin{pmatrix} 1 & 0 & 2 & 0\\ 0 & -1 & 1 & 0\\ 0 & 0 & 0 & 0\end{pmatrix}$ $\color{red}{\Rightarrow}$ $\begin{pmatrix} 1 & 0 & 2 & 0\\ 0 & 1 & -1 & 0\\ 0 & 0 & 0 & 0\end{pmatrix}$

여기에 $v_1, v_2, v_3$ 을 곱하고 $v_3$ 을 S로 둔다면 Eigen value의 해는 이렇게 나올겁니다.

$\begin{cases} v_3 = s \\ v_2 = s \\ v_1 = -2s \end{cases} \quad \rightarrow \quad 즉 \quad v = s\begin{pmatrix} -2 \\ 1 \\ 1\end{pmatrix}$

그러므로 $\gamma =1 \quad 일 때$

고유벡터 = $(-2s, s, s) \quad s \neq0$
고유기저 = $\{(-2,1,1)\}$

case 2) $\gamma = 2$

$(2I_3 - M)v = 0 \\ \Leftrightarrow \begin{pmatrix} 2 & 0 & 2 \\ -1 & 0 & -1 \\ -1 & 0 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \\ \Leftrightarrow \begin{pmatrix} 1 & 0 & 1 & |0\\ 0 & 0 & 0 & |0 \\ 0 & 0 & 0 & |0\end{pmatrix}$


$\begin{cases} x \quad + z = 0 \\ \quad 0y \quad\quad = 0 \\ \quad\quad 0z \quad = 0 \end{cases}$
이렇게 풀면 $x$와 $z$는 자유변수로 선택할 수 있습니다
즉, $y=1$일 때의 고유벡터는 다음과 같습니다
$\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}$
이어서 풀면 아래와 같은 식이 나옵니다


$v = t \begin{pmatrix} 0 \\ 1\\ 0 \end{pmatrix} + r \begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}$
여기서 고유기저는 아래와 같습니다
$\begin{pmatrix} 0 \\ 1\\ 0 \end{pmatrix}$,    $\begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}$
고유벡터는 아래와 같습니다
$\begin{pmatrix} 0 \\ t\\ 0 \end{pmatrix}$,    $\begin{pmatrix} -r \\ 0 \\ r \end{pmatrix}$

v_2가 영행렬이라 먼저 free variables로 t를 설정해주고 나머지를 r로 구합니다
어차피 해공간은 0이 나와야 합니다
v_3과 v_1는 같은벡터로 중복을 제거할겸 v_3 + v+1 = 0을 통해 합쳐주고
즉 free variables 2개를 사용하여 v의 해공간은 위와 같이 나옵니다

free variables에 대해 잘 모르겠으면 클릭 —> ✍

그러므로 $\gamma = 2$     일때는
고유벡터:    (-r, t, r)
고유기저:    {(0,1,0), (-1,0,1)}

결론:

즉 이 3x3행렬 $M = \begin{pmatrix} 0 & 0 & -2 \\ 1 & 2 & 1 \\ 1 & 0 & 3\end{pmatrix}$ 에 대해

$\gamma(고유값) = 1$   일때는
고유기저가 원소 1개인 {(-2,1,1)}

$\gamma(고유값) = 2$   일때는
고유기저가 원소 2개인 {(0,1,0), (-1,0,1)}

5-2 예제2

행렬 $A = \begin{pmatrix} 0 & -3 & -3 \\ 1 & 4 & 1 \\ -1 & -1 & 2\end{pmatrix}$   에 대해 다음 물음에 답하시오.

(1)   A를 대각화하는 행렬 P를 구하고,
대각행렬   $B = P^{-1}AP$ 를 구하시오

(2)   두행렬 A, B에 대해 본문에 제시된 10가지 닮음 불변량을 각각 확인하시오 🎨여기 클릭해서 확인

풀이

(1)-ㄱ 고윳값 구하기

$det(\gamma I_3 -A) \\ =det \begin{pmatrix} \gamma & 3 & 3 \\ -1 & \gamma-4 & -1 \\ 1 & 1 & \gamma-2\end{pmatrix} \\ \Leftrightarrow det = \gamma \begin{vmatrix} \gamma-4 & -1 \\ 1 & \gamma-2 \\ \end{vmatrix} - 3 \begin{vmatrix} -1 & -1 \\ 1 & \gamma-2 \\ \end{vmatrix} + 3 \begin{vmatrix} -1 & \gamma-4 \\ 1 & 1 \\ \end{vmatrix} \\ \Leftrightarrow \gamma(\gamma-3)^2= 0 \\ \rightarrow \gamma = 0 \quad or \quad 3$

즉 Eigenvalue $(\gamma) = 0 \quad or \quad 3$

(1)-ㄴ

$\gamma =0$   일 때

$\begin{pmatrix} 0 & 3 & 3 & |0 \\ -1 & -4 & -1 & |0 \\ 1 & 1 & -2 & |0 \end{pmatrix} \\ \Leftrightarrow \begin{pmatrix} 1 & 1 & -2 & 0 \\ 0 & -3 & -3 & 0 \\ 0 & 3 & 3 & 0 \end{pmatrix} \\ \Leftrightarrow \begin{pmatrix} 1 & 0 & -3 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}$

u로 행렬방정식을 나타내보겠습니다.     $u_1 -3u_3 = 0 \\ u_2 + u_3 = 0$

$u_3$ 를 매개변수인 t로 표현하니 나머지
$u_1, u_2$ 도 표현이 가능하더라

그러므로 $u = t \begin{vmatrix} 3 \\ -1 \\ 1\end{vmatrix}$

즉 $\gamma =0$ 일 때 고유벡터인 u의 성분은

$\begin{vmatrix} 3t \\ -t \\ t \end{vmatrix}$ 가 되더라

(1)-ㄷ

$\gamma = 3$   일 때

$\begin{pmatrix} 3 & 3 & 3 & |0 \\ -1 & -1 & -1 & |0 \\ 1 & 1 & 1 & |0 \end{pmatrix} \\ \Leftrightarrow \begin{pmatrix} 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}$

이번에는 s와 r이라는 free variables를 설정하겠습니다
$v = s\begin{vmatrix} ? \\ ? \\ ? \end{vmatrix} + r\begin{vmatrix} ? \\ ? \\ ? \end{vmatrix}$

링크 —> 왜 free variables 설정했는지 모르겠다면 여기 클릭

보아하니 첫번째 성분(1번행)과달리 2, 3번째 성분들은 0이네요.
그에 대해 2번째 성분에 대해 볼 때,   3번째 성분 = 0
3번째 성분에 대해 볼 때,   2번째 성분 = 0
이를 나타내면 아래와 같습니다.

$v = s\begin{vmatrix} -1 \\ 1 \\ 0 \end{vmatrix} + r\begin{vmatrix} -1 \\ 0 \\ 1 \end{vmatrix}$

여기서 고유기저는 $\begin{vmatrix} -s \\ s \\ 0 \end{vmatrix} + \begin{vmatrix} -r \\ 0 \\ r \end{vmatrix}$    이 2개의 성분으로 만들 수 있는 집합들을 의미합니다.

(1)-ㄹ

$P = \begin{pmatrix} 3 & -1 & -1 \\ -1 & 1 & 0 \\ 1 & 0 & 1 \end{pmatrix}$   일 때

P = A를 대각화하는 행렬
여기선 $P^{-1}$ 도 필요한데 가우스 소거법을 통해 진행하겠습니다.

방법은 P행렬 크기만큼 우측에 단위행렬을 이어줍니다
그리고 좌측 행렬을 기약행 사다리꼴로 만들면 됩니다
$P^{-1} = \begin{pmatrix} 3 & -1 & -1 & |1 & 0 & 0 \\ -1 & 1 & 0 & |0 & 1 & 0\\ 1 & 0 & 1 & |0 & 0 & 1\end{pmatrix} \\ \Leftrightarrow \begin{pmatrix} 3 & -1 & -1 & 1 & 0 & 0 \\ -1 & 1 & 0 & 0 & 1 & 0\\ 1 & 0 & 1 & 0 & 0 & 1\end{pmatrix}$

이렇게 보니 3행의 1열이 선도원소라서 첫번째행으로 올리고 3행은 아래로 내려온 후에
각각 행들을 연산해 소거 해줍니다

$\Leftrightarrow \begin{pmatrix} 1 & 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 & 1 & 1 \\ 0 & -1 & -4 & 1 & 0 & -3 \end{pmatrix} \\ \Leftrightarrow \begin{pmatrix} 1 & 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 & 1 & 1 \\ 0 & 0 & -3 & 1 & 1 & -2 \end{pmatrix} \\ P^{-1} = \begin{pmatrix} 1 & 0 & 0 & \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ 0 & 1 & 0 & \frac{1}{3} & \frac{4}{3} & \frac{1}{3} \\ 0 & 0 & 1 & -\frac{1}{3} & -\frac{1}{3} & \frac{2}{3} \end{pmatrix} \\ \Leftrightarrow P^{-1} = \frac{1}{3} \begin{pmatrix} 1 & 1 & 1 \\ 1 & 4 & 1 \\ -1 & -1 & 2\end{pmatrix}$

이제 본식에 대입해봅니다
$B = P^{-1}AP$

$= \frac{1}{3} \begin{pmatrix} 0 & 0 & 0 \\ 3 & 12 & 3 \\ -3 & -3 & 6 \end{pmatrix} \begin{pmatrix} 3 & -1 & -1 \\ -1 & 1 & 0 \\ 1 & 0 & 1 \end{pmatrix} \\ = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{pmatrix}$

(2) 링크

이것을 참고하여 증명

A 행렬,    B행렬(A를 대각화시킨 행렬)
을 아래와 같이 구했습니다.
$A = \begin{pmatrix} 0 & -3 & -3 \\ 1 & 4 & 1 \\ -1 & -1 & 2 \end{pmatrix} \quad\quad\quad B = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{pmatrix}$

1. 행렬식
B행렬은 det = 0 나오는게 너무 자명하다.
그러면 A행렬도 과연 0이 나올까?
(A행렬을 1열 방향으로 계산했음)
$detA = 0 \begin{vmatrix} 4 & 1 \\ -1 & 2 \\ \end{vmatrix} -1 \begin{vmatrix} -3 & -3 \\ -1 & 2 \\ \end{vmatrix} -1 \begin{vmatrix} -3 & -3 \\ 4 & 1 \\ \end{vmatrix} = -1(-6-3)-(-3+12) = 0 \\ detB = 0$
이로써 둘다 같습니다

2. 가역성
detA = 0,     detB = 0
즉 둘다 역행렬이 존재하지 않아 비가역성

3. rank
rankB = 2

A행렬을 기약행사다리꼴로 변환하면 rankA도 구할 수 있음
$A = \begin{pmatrix} 0 & -3 & -3 \\ 1 & 4 & 1 \\ -1 & -1 & 2 \end{pmatrix} \rightarrow \begin{pmatrix} 1 & 4 & 1 \\ 0 & 3 & 3 \\ 0 & -3 & -3 \end{pmatrix} \rightarrow \begin{pmatrix} 1 & 0 & -3 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{pmatrix}$

즉 rankA = 2

4. Nullity
nullityA = n-rankA = nullityB
3-2 = 1

5. 고유다항식
$\gamma(\gamma-3)^2= 0, \quad\quad\quad B =\begin{pmatrix} 0 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{pmatrix}$
B행렬의 대각성분과 좌측의 고유다항식을 보니 서로 일치합니다

6. 고윳값
$\gamma = 0 \quad or \quad 3$

7. 고유기저 차원
$\gamma = 0$   일 때 1개

$\gamma = 3$   일 때 2개

8. 대각성분합
A행렬:
tr(A) = 0+4+2 = 6

B행렬:
tr(B) = 0+3+3 = 6

9. 대수적 중복도
$\gamma$ 의 계수
$\gamma=0$ 일 때 1
$\gamma=3$ 일 때, 2

10. 기하적 중복도
말 그대로 기저의 원소 갯수
링크 참조

5-3 예제3

행렬 $M =\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & -3 & 3 \end{pmatrix}$    에 대하여 행렬
$3M^5-5M^4$ 를 케일리 해밀턴 정리를 이용해 구하시오.

케일리 해밀턴 정리
필요한것: -고유다항식-

step 1    고유다항식 찾기
$f(\gamma) = det(\gamma I_3 -M) \\ det = \begin{pmatrix} \gamma & -1 & 0 \\ 0 & \gamma & -1 \\ -1 & 3 & \gamma-3 \end{pmatrix}$
1열로 det 정리하면 될 듯
$detM = \gamma \begin{vmatrix} \gamma & -1 \\ 3 & \gamma-3 \\ \end{vmatrix} -0 \begin{vmatrix} -1 & 0 \\ 3 & \gamma-3 \\ \end{vmatrix} -1 \begin{vmatrix} -1 & 0 \\ \gamma & -1 \\ \end{vmatrix} \\ \Leftrightarrow \gamma^3-3\gamma^2+3\gamma-1 \\ \Leftrightarrow M^3-3M^2+3M-I_3 = 0$

이것을 $M^3$ 에 대해 정리하면 아래와 같이 됩니다.

$M^3 = 3M^2-3M+I_3$



step 2    수식 변환 응용
방금 위의 식에 M을 곱하면 아래처럼 됩니다.
$M^4 = 3M^3 - 3M^2 + M$

이 식에서 $M^3$ 에 대해 계산한 것을 대입하면 됩니다
계산하면 이렇게 정리가 가능합니다
$M^4 = 3(3M^2 - 3M + I_3) -3M^2 + M \\ \Leftrightarrow M^4 = 6M^2 -8M +3 I_3 \\ M^5 = MM^4 = M(6M^2 -8M +3 I_3)$
$\color{red}{\Rightarrow}$ $(6M^3 -8M^2 +3M)$
이 식에 아까구했던 $M^3$ 에 대한 수식을 대입하면 됩니다

$M^5 = 6(3M^2-3M+I_3) - 8M^2 + 3M \\ \Leftrightarrow M^5 = 10M^2 - 15M + 6I_3$

이로써 $M^5 \quad M^4$ 를 둘다 구했으니 이제 문제에 맞춰 각각 변형시킵시다
$\Leftrightarrow 3M^5-5M^4 \\3(10M^2 - 15M + 6I_3) \quad - \quad 5(6M^2 -8M +3 I_3) \\ \Leftrightarrow -5M + 3I_3$

결과

준식:    $-5M + 3I_3 = \begin{pmatrix} 3 & -5 & 0 \\ 0 & 3 & -5 \\ -5 & 15 & -12 \end{pmatrix}$

참고

1. [선형대수학] 5강. 고윳값과 대각화
2. 혁펜하임     [선대] 5-2강. 고윳값 분해 (Eigendecomposition) 의 모든 것!
3. [장황수학]    고유치 및 고유벡터
4. [장황수학]    고유치 및 고유벡터의 성질
5. [장황수학]    닮은 및 대각화 행렬
6. [공돌이의 수학정리노트 (Angelo’s Math Notes)]     고윳값과 고유벡터