[선형대수학] 6강. 복소벡터공간
🙅♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
<목차>
0. 들어가며
1. 복소벡터공간
1-1 정의
1-2 복소켤레(complex conjugate)
1-3 대수적 성질
2. 복소내적공간
2-1 정의
2-2 성질
3. 복소고윳값과 복소고유벡터
4. 용어 정리
4-1 켤레 전치행렬(에르미트 전치행렬)
4-2 에르미트행렬(Hermitian matrix )
4-3 유니터리행렬(Unitary matrix)
4-4 정규행렬(Normal matrix)
5. 유니터리 대각화(unitary diagonalization)
0. 들어가며
6강 전까지는 실수 벡터공간에 관한 내용이었으며,
이번에는 조금 더 상위 개념인 복소벡터공간에 대해 학습하는 시간을 가져보겠습니다.
1. 복소벡터공간
🔍요약
\(C^n\)이 실수를 스칼라배하는 벡터공간이라면 차원은 2n
$ \color{pink}{\Rightarrow} $ 보통 기저는 \(\begin{pmatrix} 1 \\ 0 \end{pmatrix}\), \(\begin{pmatrix} 0 \\ 1 \end{pmatrix}\), \(\begin{pmatrix} i \\ 0 \end{pmatrix}\), \(\begin{pmatrix} 0 \\ i \end{pmatrix}\)
\(C^n\)이 복소수를 스칼라배하는 벡터공간이라면 차원은 n
$ \color{pink}{\Rightarrow} $ 보통 기저는 \(\begin{pmatrix} 1 \\ 0 \end{pmatrix}\), \(\begin{pmatrix} 0 \\ 1 \end{pmatrix}\)
1-1 정의
쉽게 얘기하여 스칼라가 복소수인 벡터공간
모든 복소 n-튜플 \((v_1, v_2, ..., v_n)\) 의 집합을 복소 n-공간이라 하고,
\(c^n\) (n차원 복소벡터공간)으로 표시한다.
1-2 복소켤레(complex conjugate)
복소켤레는 실수부(\(Re(v)\))와 허수부(\(iIm(v)\))로 나뉜다.
\(C^n\) 의 임의의 벡터
\(v = (v_1, v_2, ..., v_n) \\ =(a_1 + b_1i,\quad a_2+b_2i, ... a_n+b_ni) \\ = (a_1, ..., a_n) +i(b_1, ..., b_n) \\ =Re(v) + iIm(v)\)
에 대하여
v의 복소켤레 \((\bar v)\)
\(\bar v = (\bar v_1, \bar v_2, ..., \bar v_n) \\ =Re(v)- iIm(v)\)
즉 복소켤레는 실수부-허수부 (실수부에서 허수부 뺀 것)
예제(2개)
ex-1) \(v=(1+i,\quad -i,\quad 3,\quad 3i)\) 에 대하여
\(Re(v), \quad Im(v), \quad \bar v\) 를 각각 구하시오
\(Re(v)\) = (1, 0, 3, 0)
\(Im(v) =\) (1, -1, 0, 3)
\(\bar v = Re(v) - iLm(v) \\ = (1-i, \quad i, \quad 3, \quad -3i)\)
ex-2) \(A = \begin{pmatrix} 1-i & 2i \\ -1 & 3+2i \end{pmatrix}\) 에 대하여
\(\bar A, \quad det(\bar A)\) 를 각각 구하시오
\(\bar A = \begin{pmatrix} 1+i & -2i \\ -1 & 3-2i \end{pmatrix} \\ det(\bar A) =(3-2i+3i+2)-(2i) \\ = 5-i\)
1-3 대수적 성질
\(C^n\) 의 벡터 u, v와 스칼라 k에 대해
1) \(\bar{\bar{u}} = u\)
2) \(\bar{ku} = \bar k \bar u\)
3) \((\overline{u \pm v}) = \bar u \pm \bar v\) (복부호 동순)
mxk 행렬 A와 kxn 행렬 B에 대해
1) \(\bar{\bar{A}} = A\)
2) \(\overline {(A^T)} = (\bar A)^T\)
3) \(\overline {AB} = \bar A \bar B\)
😀증명 \(\overline {AB} = \bar A \bar B\)
\(A = \begin{pmatrix} 1-i & 2i \\ -1 & 3+2i \end{pmatrix} \quad\quad B = \begin{pmatrix} i & 1-i \\ 0 & -1 \end{pmatrix}일 때 \\ \bar A = \begin{pmatrix} 1+i & -2i \\ -1 & 3-2i \end{pmatrix}, \bar B = \begin{pmatrix} -i & 1+i \\ 0 & -1 \end{pmatrix} \\ AB = \begin{pmatrix} i+1 & -2i-2i \\ -i & -1+i-3-2i \end{pmatrix} = \begin{pmatrix} 1+i & -4i \\ -i & -4-i \end{pmatrix} \\ AB \quad 전체에 \quad 켤레를 \quad 씌우면 \rightarrow \overline {AB} \\ \bar A \bar B = \begin{pmatrix} -i+1 & 2i+2i \\ i & -1-i-3+2i \end{pmatrix} = \begin{pmatrix} 1-i & 4i \\ i & -4+i \end{pmatrix}\)
이렇게 보니 AB에 켤레를 씌우면 \(\overline {AB}\) 가 되는데 이는 \(\bar A \bar B\) 랑 결과가 같아지는게 보인다
2. 복소내적공간
2-1 개념
참고
깃허브 markdown에서 \(\cdot\)에 색깔을 입힐 수 없어 *로 대체합니다
*→ 스칼라배
* → 점곱(dot product)
복소벡터공간 ( \(V, C, +,\) *)의 두 벡터
\(u = (u_1, u_2, ... u_n), \quad v=(v_1, v_2, ..., v_n)\)
의 내적 <u, v>: V x V → C 은
\(<u,v> = u\)*\(v = u_1 \bar v_1 + u_2 \bar v_2 + ... + u_n \bar v_n\) 로 정의한다.
또한 내적이 정의되어 있는 복소벡터공간을 복소내적공간이라 한다
빠른 이해
\(v = (1, i)\\ ||v|| = \sqrt{v \cdot \bar v} = \sqrt{(1,i) \cdot (1,-i)} = \sqrt{1+1} \\ = \sqrt 2\)
복소평면으로 복소벡터\(\begin{bmatrix}1 \\ -i\end{bmatrix}\)를 표현하면
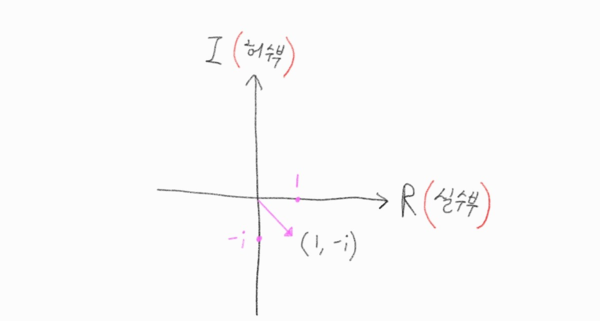
위의 2차원 복소평면좌표 그래프를 봤을 때 Norm을 기하적으로 해석하면
분홍색 벡터(분홍색 화살표)의 길이, 정확하게 \(\sqrt 2\)가 나와서
Norm의 연산이 n차원의 복소평면에서도 부드럽게 정의가 된다고 볼 수 있다.
2-2 성질
복소내적공간의 세백터 u, v, w와 스칼라 k에 대해 다음 내적결과에 대한 4가지 성질이 만족한다.
- <u, v> = \(\overline {<v, u>}\)
- \(<u+v, w> = <u,w> + <v,w> \\ <u, v+w> = <u,v> + <u,w>\)
- \(<ku, v> = k<u,v> \\ <u, kv> = \bar k< u,v>\)
- \(v \neq \vec{0}\)
일 때 <v, v> >0
4번 증명
\(v=(a_1+b_1i, \quad a_2+b_2i, ... , a_n=b_ni) \neq 0 \\ v \cdot v = (\quad\quad) \cdot(a_1-b_1i, \quad a_2-b_2i, .., a_n-b_ni) \\ = ({a_1}^2 + {b_1}^2) + ({a_2}^2 + {b_2}^2)+...+({a_n}^2 + {b_n}^2) > 0\)
즉 확인하니 0보다 크다는건 자명하겠더라
3. 복소고윳값과 복소고유벡터
3-1 정의
복소정사각행렬 A에 대하여 고유방정식 \(det(\gamma I-A)=0\) 의 복소해 \(\gamma\)를 A의 복소고윳값 이라 한다
또한 \(Av = \gamma v\) 를 만족시키는 모든 벡터 v의 집합을 A의 고유공간,
고유공간의 0벡터가 아닌 벡터를 A의 복소고유벡터 라고 한다.
ex) \(A = \begin{pmatrix} 2 & 1 \\ -5 & -2 \end{pmatrix}\)
\(det(\gamma I_2 -A) = det \begin{pmatrix} \gamma-2 & -1 \\ 5 & \gamma+2 \end{pmatrix} \\ \gamma^2+1= 0 \\ \rightarrow \gamma = \pm i\)
\(\gamma =i\) 일 때
\(\begin{pmatrix} i-2 & -1 & |0 \\ 5 & i+2 & |0 \end{pmatrix} \rightarrow\) 실수화를 위해 1행에 (i+2) 곱함 \(\begin{pmatrix} -1-4 & -i-2 & 0 \\ 5 & i+2 & 0 \end{pmatrix} \rightarrow \begin{pmatrix} 1 & \frac{i+2}{5} & 0 \\ 0 & 0 & 0 \end{pmatrix}\)
여기서 2번째 행인 \(v_2 = (0, 0, 0)\) 를 1, 즉 t로 변경하고 v의 해공간은 아래와 같아진다
\(v = t \begin{bmatrix} -\frac{i+2}{5} \\ 1\end{bmatrix}\)
즉 고유공간의 기저 = \(\left\{ \left( -\frac{i+2}{5}, \quad 1 \right) \right\}\)
고유벡터 \(\left\{ \left( -\frac{i+2}{5}t, \quad t \right) \right\} \quad (t \neq0)\)
\(\gamma =-i\) 일때 이건 생략
3-2 정리
\(\gamma\) 가 실 정사각행렬 A의 고윳값이고 v는 이에 대응하는 고유벡터면,
\(\bar \gamma\) 또한 A의 고유값이며 \(\bar v\) 는 이에 대응하는 고유벡터다
😀증명
\(Av = \gamma v \\ \leftrightarrow \overline {Av} = \bar \gamma \bar v \\ \leftrightarrow A \bar v = \bar \gamma \bar v \\ v \neq \vec{0} \rightarrow \bar {v} \neq \vec{0}\)
$\color{pink}{\downarrow}$
$\color{pink}{\downarrow}$
\(\gamma= 1+i\\ \bar \gamma = 1-i\)
4. 용어정리
4-1 켤레 전치행렬(에르미트 전치행렬)
\(A^H\) 라고도 하며 복소행렬 A의 전치행렬을 구한 후에, 각 성분을 켤레인 복소수로 바꾼 행렬
영어 표기는 conjugate transpose matrix or Hermitian transpose matrix
특징
복소 스칼라 k와 mxr행렬 A, rxn행렬 B에 대해 다음 4가지 특징이 성립한다
1) \((A^H)^H = A\)
2) \((A \pm B)^H = A^H \pm B^H\) (복부호 동순)
3) \((KA)^H = \bar kA^H\)
4) \((AB)^H = B^HA^H\)
🎲4)번 증명
\(ex)\) \(A = \begin{pmatrix} 1 & i \\ 1-i & -1 \end{pmatrix} \quad\quad B = \begin{pmatrix} 1+i & -1 \\ -i & 2 \end{pmatrix}\)
\(AB = \begin{pmatrix} 2+i & -1+2i \\ 2+i & -3+i \end{pmatrix} \\ \therefore (AB)^H = \begin{pmatrix} 2-i & 2-i \\ -1-2i & -3-i \end{pmatrix}\)
\(B^HA^H = \begin{pmatrix} 1-i & i \\ -1 & 2 \end{pmatrix} \begin{pmatrix} 1 & 1+i \\ -i & -1 \end{pmatrix} = \begin{pmatrix} 2-i & 2-i \\ -1-2i & -3-i \end{pmatrix}\)
즉 \((AB)^H = (BA)^H\) 성립한다
4-2 에르미트행렬(Hermitian matrix )
행렬 A가 있다고 가정할 때,
\(A = A^H\) 가 성립하는 복소정사각행렬
4-3 유니터리행렬(Unitary matrix)
복소행렬들을 다룰 때 주로 쓰인다
특징으로 복소정사각행렬 A의 역행렬 \(A^{-1}\) 에 대하여 \(A^{-1} = A^{H}\) 가 성립하는 행렬 A
4-4 정규행렬(Normal matrix)
유니터리 대각화에 사용되고 아래와 같은 조건을 만족한다
\(AA^{H} = A^{H}A\) 가 성립하는 복소정사각행렬 A
ex) 에르미트행렬, 유니터리행렬
5. 유니터리 대각화(unitary diagonalization)
유니터리 대각화 가능한 행렬은 정규행렬이며, 그 역도 성립한다.
즉 정규행렬은 유니터리 대각화가 가능하다
\(P^{H}AP = D\)
1
2
3
4
# 참고
A: 복소정사각행렬
P: A를 유니터리 대각화하는 유니터리행렬
D: 복소대각행렬
여기서 활용해볼 것 \(P^{-1} = P^{H}\)
🧔♂️에르미트행렬A의 유니터리 대각화과정
1
2
3
4
5
6
7
8
9
step1:
A의 모든 고유공간의 기저를 구한다
step2:
고유공간의 정규직교기저를 구한다
step3:
기저벡터를 열벡터로 하는 행렬 P는
유니터리행렬이고, A를 대각화한다
ex) \(A =\begin{pmatrix} 1 & 1+i \\ 1-i & 0 \end{pmatrix}\)을 대각화하자
1. 고윳값 구하기
\(det(\gamma I_2-A) = det \begin{pmatrix} \gamma-1 & -1-i \\ -1+i & \gamma \end{pmatrix} \\ = \gamma^2-\gamma-2 = 0 \\ = (\gamma-2)(\gamma+1) = 0 \\ \gamma = -1 \quad or \quad 2\)
2. \(\gamma = -1\)일 때
2번째 행에 (-1-i) 곱해주어 gaussian elimination 한 후 1번행에서 \(-\frac{1}{2}\) 곱해주자 \(\begin{pmatrix} -2 & -1-i & 0 \\ -1+i & -1 & 0 \end{pmatrix} \rightarrow \begin{pmatrix} 1 & \frac{1+i}{2} & 0 \\ 0 & 0 & 0 \end{pmatrix}\)
즉 \(\gamma = -1\) 일때의 고유벡터는 \(v = \begin{pmatrix} -\frac{1+i}{2}t & t \end{pmatrix} \quad\quad (t \neq 0)\)
여기에 보기 좋게 t=2 대입하여 기저를 보기 쉽게(1+i, -2)로 변환합니다
3. \(\gamma = 2\)일 때
2행에 (-1-i) 곱해주면 1행과 2행은 같아져 2행 소거합니다.
그리고 보기좋게 t=1 대입합니다.
\(\begin{pmatrix} 1 & -1-i & 0 \\ -1+i & 2 & 0 \end{pmatrix} \rightarrow \begin{pmatrix} 1 & -1-i & 0 \\ 2 & -2-2i & 0 \end{pmatrix} \rightarrow \begin{pmatrix} 1 & -1-i & 0 \\ 0 & 0 & 0 \end{pmatrix} \\ v = \left( (1+i)t, \quad t \right) \\ =기저 \left( 1+i, \quad 1 \right)\)
4. 정규직교기저
원래라면 1~3의 과정에서 구한 기저들로 직교화가 되도록 임의로 설정해줘야 한다.
근데 여기서는 \(\gamma=-1\) 일때랑 \(\gamma=2\) 일때는 각각 기저1개라 직교를 고려하지 않아도 된다.
왜냐하면 직교를 고려하려면 기저가 아래의 예시처럼 되야한다
\(v = t \begin{bmatrix} 1 \\ 0 \end{bmatrix} + s \begin{bmatrix} 0 \\ 1 \end{bmatrix}\)
그리하여 여기서는 정규화만 시키겠다
(정규화: 벡터의 norm을 1로 맞추는 것이다)
아까 \(\gamma=-1\) 일때랑 \(\gamma=2\) 일때 구한 기저들을 \(v_1\), \(v_2\)라 하겠다
(너무 당연한 사실이지만 복소수벡터를 norm연산할때 켤레를 취해줘야한다.)
정규화
\(||v_1|| = \sqrt{(1+i, \quad -2) \cdot (1-i, \quad -2)} \\ = \sqrt{1+1+4} \rightarrow \sqrt 6 \\ \therefore \left( \frac{1+i}{\sqrt 6}, \quad -\frac{2}{\sqrt 6} \right)\)
\(||v_2|| = \sqrt{(1+i, \quad 1) \cdot (1-i, \quad 1)} \\ = \sqrt{2+1} \rightarrow \sqrt 3 \\ \therefore \left( \frac{1+i}{\sqrt 3}, \quad \frac{1}{\sqrt 3} \right)\)
5. 유니터리행렬 대각화
아까 구한 normalized \(v_1\)과 \(v_2\)를 전치시켜 P(유니터리행렬)을 만들자
\(P = \begin{pmatrix} \frac{1+i}{\sqrt 6} & \frac{1+i}{\sqrt 3} \\ -\frac{2}{\sqrt 6} & \frac{1}{\sqrt 3} \end{pmatrix} \\ P^H = \begin{pmatrix} \frac{1-i}{\sqrt 6} & -\frac{2}{\sqrt 6} \\ \frac{1-i}{\sqrt 3} & \frac{1}{\sqrt 3} \end{pmatrix} \\ D = P^HAP = \begin{pmatrix} \frac{1-i-2+2i}{\sqrt 6} & \frac{1+1}{\sqrt 6} \\ \frac{1-i+1-i}{\sqrt 3} & \frac{1+1}{\sqrt 3} \end{pmatrix} \cdot P \\ = \begin{pmatrix} \frac{-1+i}{\sqrt 6} & \frac{2}{\sqrt 6} \\ \frac{2-2i}{\sqrt 3} & \frac{2}{\sqrt 3} \end{pmatrix} \cdot P = \begin{pmatrix} \frac{-1-1-4}{6} & \frac{-1-1+2}{\sqrt 18} \\ \frac{2(1+1)-4} {\sqrt 18} & \frac{2(1+1)+2}{3} \end{pmatrix} \\ \therefore D = \begin{pmatrix} -1 & 0 \\ 0 & 2 \end{pmatrix}\)
이렇게 대각행렬 D를 도출했으며,
전체 과정을 요약하면 A라는 Hermitian matrix의 unitary diagonalization을 통해
D라는 diagonal matrix를 볼 수 있었다.
정확하게 말하자면 D를 복소대각행렬(complex diagonal matrix)이라고 할 수 있겠다.

