Orthogonality of The Four Subspaces

🙅‍♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다

<목차>

1. 들어가며
2. 복습
 2-1) 정의역, 공역, 치역
 2-2) 선형변환
 2-3) 부분공간
3. 행공간과 열공간
4. 영공간
5. 좌영공간
6. 과제

1. 들어가며

이번 시간에는 4개의 주요 부분공간의 관계들을 이해해보는 시간을 가질 것입니다.

1. 열공간(Column space)
2. 행공간(Row Space)
3. 영공간(Null Space)
4. 좌영공간(Left Null Space)

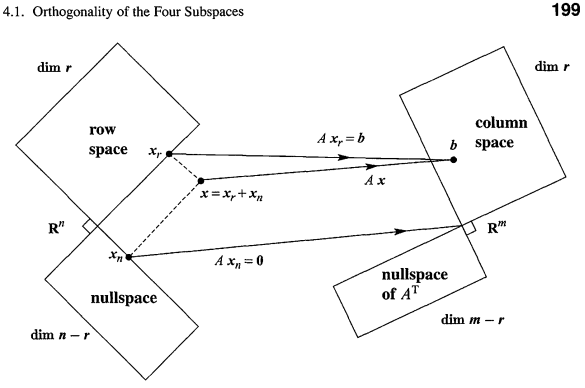
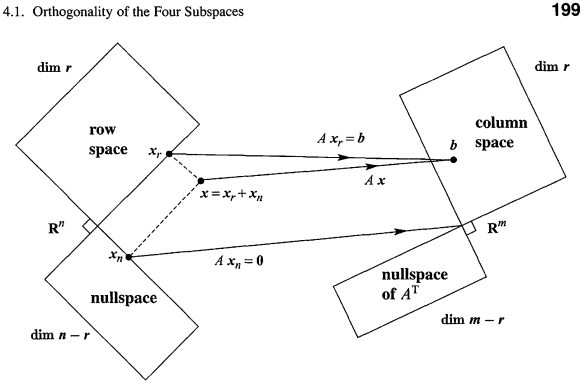
이 4개의 주요공간들을 이해함으로써 아래 도식화를 이해할 수 있게 되고,
나아가 이는 어떻게 사진(무시쿵야)에 형성되어있는지 알 수 있게될 것입니다.

2. 복습

2-1 정의역, 공역, 치역

우선 정의역, 공역, 치역을 잘 모른다면 이 링크로 들어가서 참고합시다

https://joonk2.github.io/assets/img/math/LinearAlgebra/part4/1.png

선형대수에서 정의역, 공역, 치역?
—> 그럼 선형변환에서 말하는 정의역, 공역, 치역은 어떤 것일까?

2-2 선형변환

🔍링크 ㄱㄱ

2-3 부분공간

• 벡터공간 벡터를 원소로 하는 집합(set)
  

• 부분공간

  1. 부분 집합의 개념을 벡터 공간에 접목한 것
     
  2. 벡터 공간의 기본 구조를 그대로 유지하는 작은 벡터공간

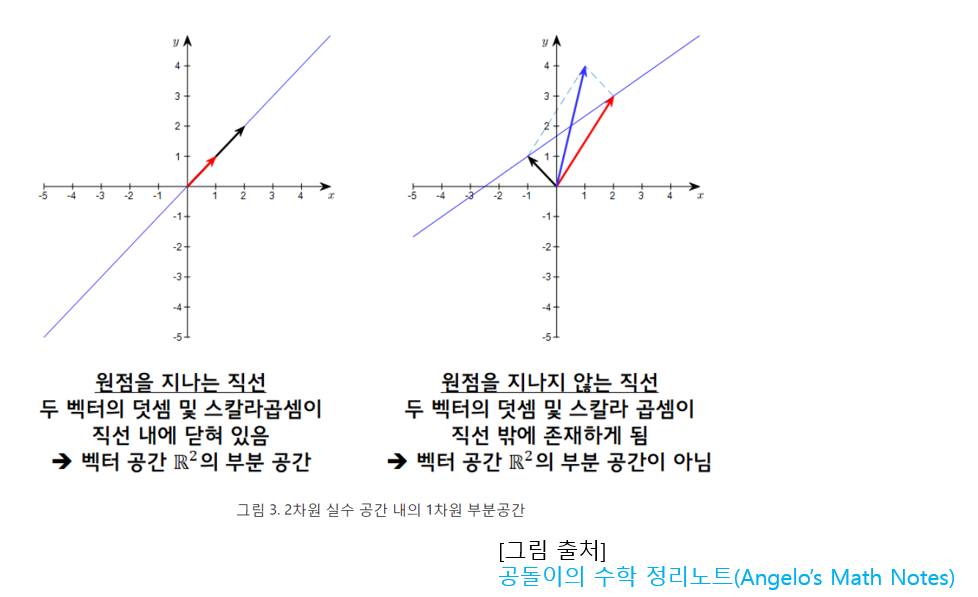
\(\vec{0}\)은 항상 벡터공간에 들어있어야 하기에
원점을 지나는 직선이 \(R^2\)(2차원) 벡터공간 상에서 부분 공간이 될 수 있다!

3. 행공간과 열공간

임의의 행렬 A의 모든 행 혹은 모든 열들의 선형결합(span)으로 얻은 모든 벡터를 포함하여 구성된 벡터공간은 부분 공간이며, 각각을 행공간, 열공간이라 한다.
가령 아래와 같은 행렬 A에 대해서,
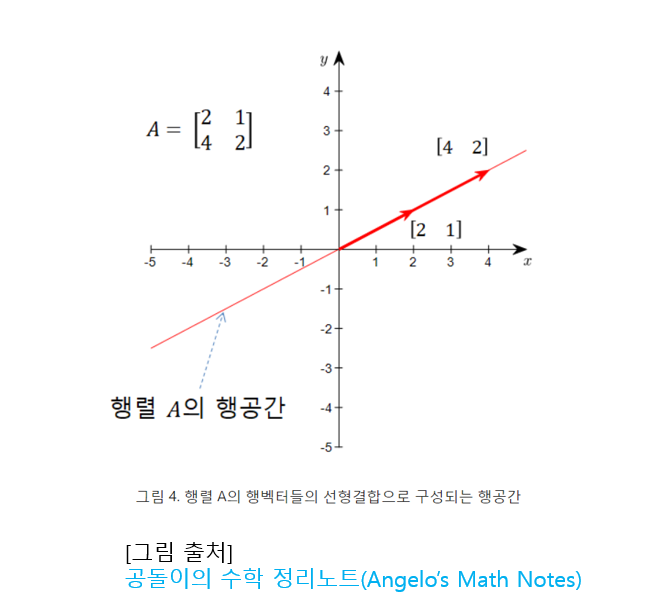
\(A=\begin{bmatrix} 2 & 1 \\ 4 & 2\end{bmatrix}\) 그러면, 행공간은 행벡터[2 1]와 [4 2]의 선형결합으로 이뤄진 선상에 있는 모든 벡터들의 집합이다

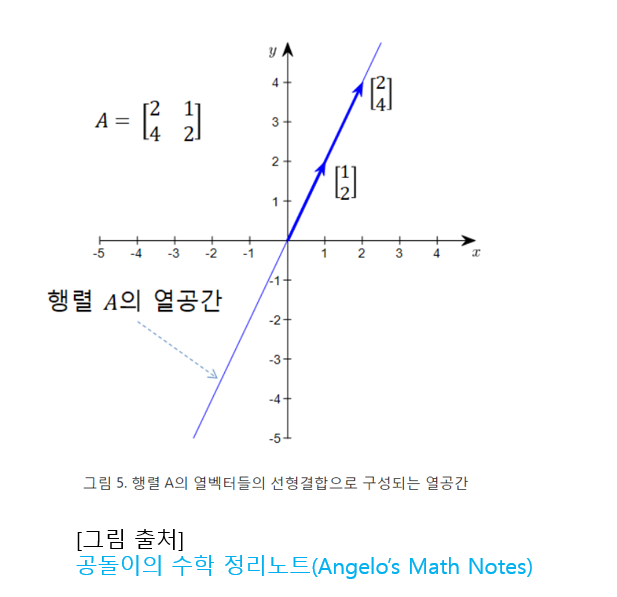
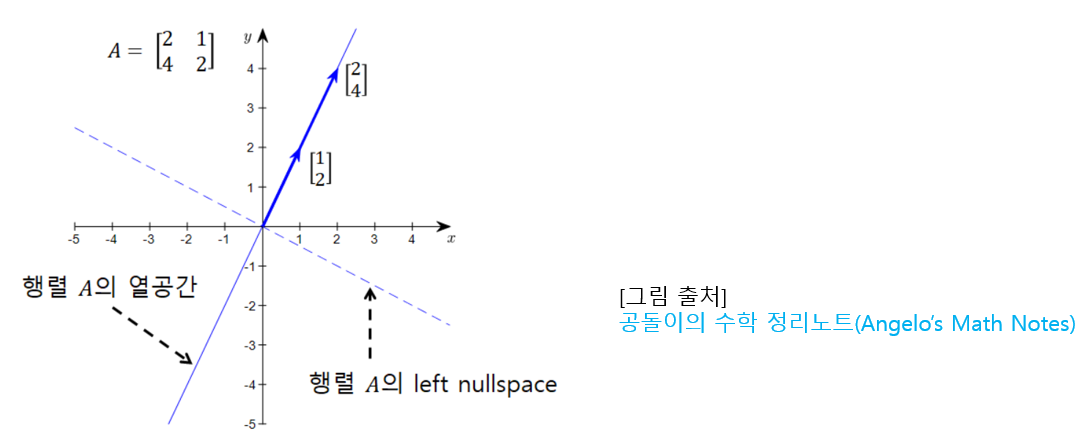
열공간은 열벡터 \([2 \quad 4]^T\) 와 \([1 \quad 2]^T\) 의 선형결합으로 이뤄진 선 상에 있는 모든 벡터들의 집합
여기서는 열벡터 2개로 선형결합 시켜서 얻을 수 있는 벡터공간을 열공간이라 한다

이렇게 보니 행공간과 열공간은 다르게 생긴 것을 확인할 수 있었다.
linear combination of row vectors → row space
linear combination of column vectors → column space

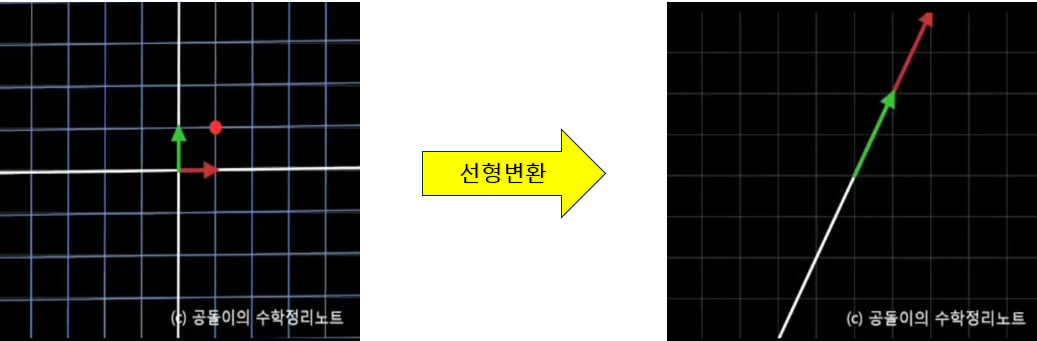
그러면, 우선 A라는 행렬의 선형변환이 어떻게 작동하는지 시각적으로 생각해보자
\(A= \begin{bmatrix} 2 & 1 \\ 4 & 2\end{bmatrix}\)
\(Ax = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x_1 \\x_2 \end{bmatrix} = \begin{bmatrix} a \\ c \end{bmatrix}x_1 + \begi{bmatrix} b \\ d \end{bmatrix}x_2\)

열벡터방향, 행벡터 방향으로 봐도 둘다 평행하다 즉 선형종속
즉 한쪽이 스칼라배를 해준 것을 알 수 있다.
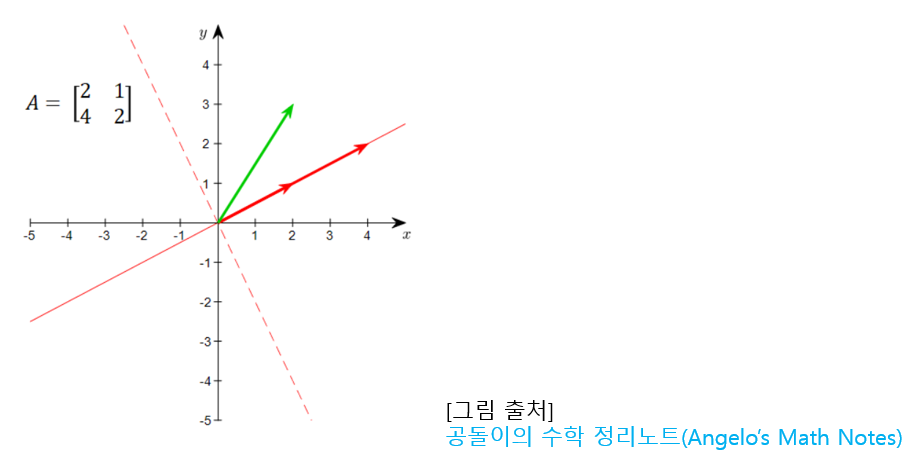
아래 그림은 초록색 선이 열벡터 \(1\begin{bmatrix} 1 \\ 2 \end{bmatrix}\)

빨간색 선이 열벡터 \(2\begin{bmatrix} 1 \\ 2 \end{bmatrix}\)

4. 영공간

개념:
행렬 A의 영공간은 다음과 같은 조건을 만족하는 \(\vec{x}\) 들의 집합

\(A \vec{x} = 0\)
즉, A라 행렬을 통해 선형변환 후, 모두 0을 출력하게 만들어주는 입력벡터 \(\vec{x}\)들이라는 것

[잠깐!] 선형변환 = 모든 입력 벡터들이 열공간으로 매핑된다

영공간이 물어보는 것:
A라는 선형변환 후에 결과가 0이 되어버리는 \vec{x}의 집합은 어디인가?
➡️ 노란색 선

위의 사진을 보고 알 수 있는 것:

행공간과 영공간은 서로 직교한다
즉 행벡터들과 직교하는 모든 공간을 잇는게 영공간이다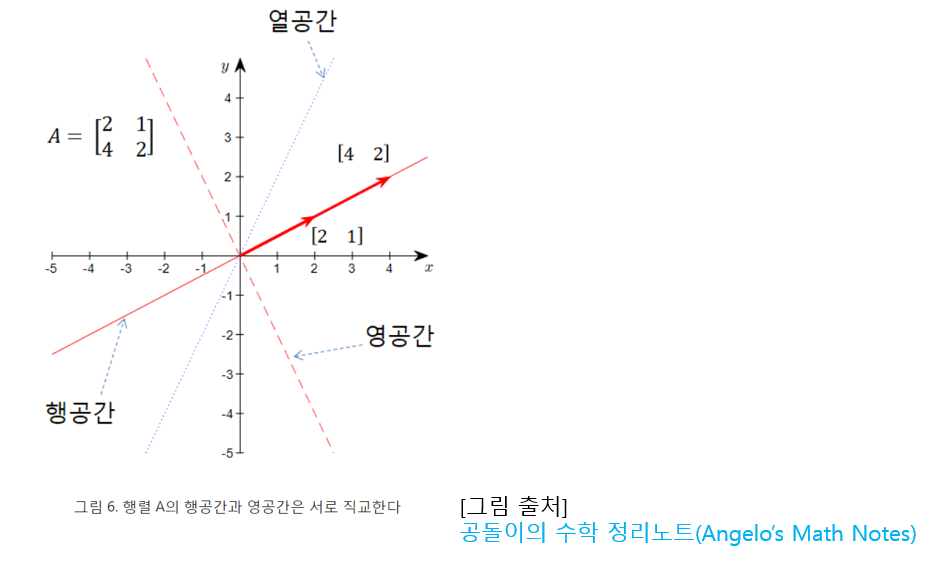

5. 좌영공간

이 그림의 우측에 보면 열공간과 좌영공간인 A행렬을 전치시킨 영공간이 서로 직교(직각표시)
즉 공간에서는 총 2쌍이 직교함

6. 과제

행렬이 함수라면, 그 함수의 기본적 의미인 집합 간의 관계를 어떻게 정의할 것인가?

For \(A \in R^{m*n}, \quad\quad f: R^n \rightarrow R^m\)

풀이:

m*n 행렬에서 전체 입력인 n차원은 row space, null space로 구성
위의 그림을 보면 nullspace의 벡터들은 선형변환 후에 도달하는 곳에서 모두 0이 된다(화살표 참고)
why? —> 직교니까

row space의 벡터들이 column space로 이동한다
근데 row space와 null space의 벡터를 합쳐서 이동해도 column space로 이동한다
why —> 말했듯이 null space의 벡터들은 선형변환 후에 모두 0이 되기 때문

입력(정의역)

row space + null space = \(R^n\)

• 선형변환의 정의역은 row space + null space의 합집합
• n차원 실수 공간상 어떤 벡터라도 row space와 null space 상의 벡터들의 선형조합으로 표현 가능

이 그림은 행공간인 빨간색 선과 영공간인 빨간 점선이 만나
치역에 해당하는 부분인 초록색인 열공간에서의 열벡터
\(1\begin{bmatrix} 1 \\ 2 \end{bmatrix}\)를 표현했고, 나아가 \(2\begin{bmatrix} 1 \\ 2 \end{bmatrix}\)도 표현할 수 있습니다.

공역

m차원 실수 공간

• 선형 변환의 치역은 column space고, 공역에서 치역을 뺀 것이 left null space
• column space와 left null space는 직교
• left nullspace는 선형 변환 과정에서 시각화 할 수는 없지만 열공간과 서로 직교하므로 다음과 같이 표현할 수 있다
  

아까 정의역 에서 행공간과 영공간에서 선형변환을 통해 생성된 초록색 선이 여기서는
파란색 선인 열공간의 열벡터입니다.

참고

[[공돌이의 수학정리노트]     4개 주요 부분 공간 간의 관계]

[[공돌이의 수학정리노트]     행렬과 선형 변환의 관계]