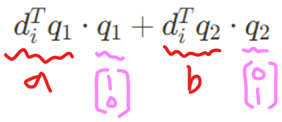PCA

🙅‍♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다

<목차>
1. PreRequisites
2. PCA 
 2-1. PCA란?
 2-2. PCA증명 (좀 길다)
  (1) 😋minimize(최소화)
  (2) 🧏‍♀️maximize
3. PCA 응용
 3-1. 차원축소(예시)
 3-2. 차원축소(영상)

1. PreRequistes

1. Eigen decompostion
   
2. Lagrange Multiplier
   
3. LSM
   
4. covariance matrix
   
   

2. PCA

2-1. PCA란?

목표:

차원 축소를 할 때 원 데이터의 분산을 보존할 것

개념:

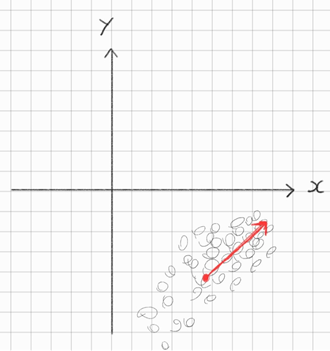
좌표값들이 하나의 데이터다 그래서 여러 개의 데터가 분포를 이루고 있음
여기서 데이터 분포의 평균으로부터 시작해 데이터의 분포를 가장 잘 설명해주는 방향을 PCA라 한다.
즉 목표를 재정의하자면 다시말해 \(\color{red}{\nearrow}\)의 벡터를 찾아 차원축소를 해야한다

예시:

만약 내가 찾은 주성분 벡터에 데이터들을 확대해서 봤을 때,
1차원 축으로 데이터들을 정사영 시켰다고 하자

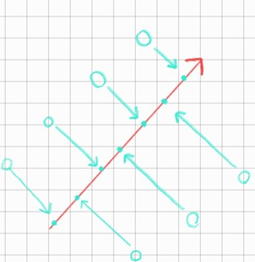
차원 축소 (2D \(\Rightarrow\) 1D)

결론:

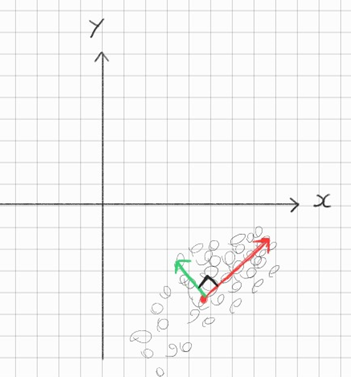
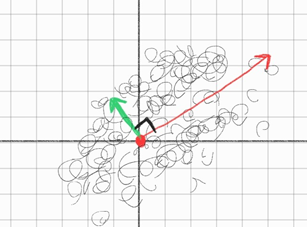
위의 개념을 토대로 이 분포의 분산이 가장 큰 방향인 \(\color{red}{\nearrow}\)가 이 분포를 가장 잘설명하는 방향이고,
그리고 두 번째로 분산이 크고 첫번째 주성분과 orthogonal 한 방향인 \(\color{green}{\nearrow}\)가 2번째로 잘 설명한다.

2-2. PCA증명 (좀 길다)

당연하게 받아들이지말고 PCA 개념에 대해 질문을 던져보자
---------------질문-----------------
1️⃣ 왜 분산이 가장 큰 방향이 이 분포를 잘 설명하는가?
2️⃣ 왜 그다음으로 잘 설명하는 방향은 첫 번째 주성분에 수직하냐?
-----------------------------------------

자 주성분분석 증명을 처음부터 차근차근 시작해보자
우선 평균으로부터 출발해 가장 분포를 잘 설명하는 방향을 찾아야하니
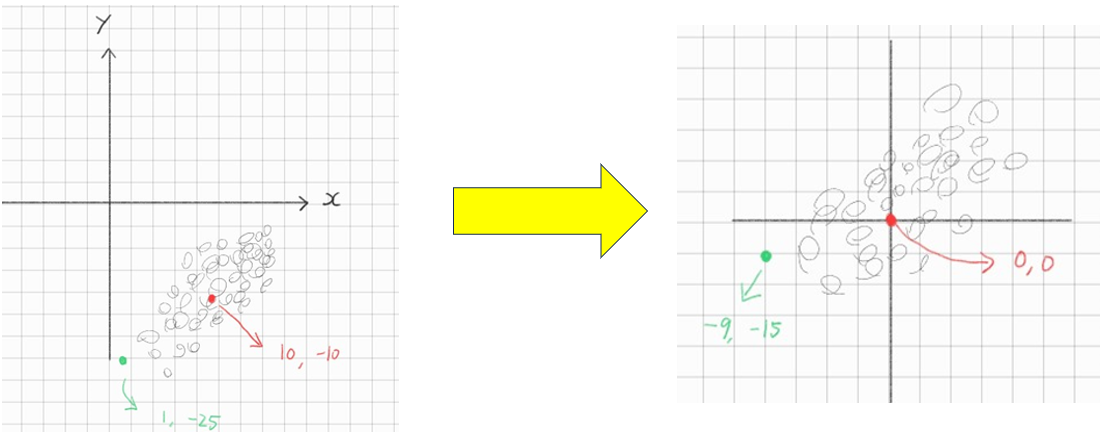
현재 4사분면에 있는 분포들의 평균이 0이 되도록 분포의 중간점을 기준에서 원점으로 옮기자
이게 무슨 말이냐면 아래 그림 참고

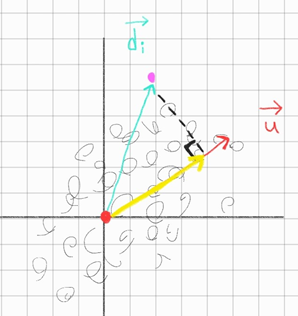
다시 본론으로 넘어가서 아래 그림을 보자

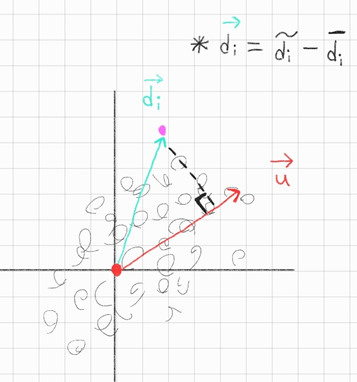
자 이제 x,y 분포들에 있는 n개 중에서 i번째 데이터를 $d_i$ 라 하자     \(d_i = \begin{bmatrix} x_i \\ y_i\end{bmatrix}\)
평균을 빼지 않은 것은 이렇게 나타내자     \(\tilde{d_i} \color{blue}{=} \begin{bmatrix} x_i \\ y_i\end{bmatrix}\)
평균을 뺀 것을 이렇게 —>   \(\bar{d_i} \color{red}{=} \begin{bmatrix} \bar{x_i} \\ \bar{y_i}\end{bmatrix}\)
그리고 위의 2번째 그래프를 보면 x, y값의 분포를 나타낸 것이 \(\ddots\ddots\ddots\ddots\cdots \color{pink}{\bullet}\) 이렇게 여러 개의 점들로 있는데
그 평균을 싹 구해 대입한 것이 \(\bar{d_i} = \begin{bmatrix} \bar{x_i} \\ \bar{y_i}\end{bmatrix}\) 이것이기도 하다

(1) 😋minimize(최소화)

잠깐 영상을 참고하자

(이 영상은 모든 분포들의 최소 error를 찾는 것, 즉 주성분을 찾는 과정이다)

자 원래는 x,y 분포들이 있을 때 모든 점들과 비교하여 error(값)이 가장 작을 때가 언제인지 비교하는게 맞는데 그러면 너무 할게 많아지므로 나는 점 하나만 보겠다
그러면 이제부터 orthogonal하면서 error가 가장 적은 점과 연결해야하는데 임의의 x,y를 가진 \(\color{pink}{\bullet}\)점을 향하는 벡터가 있을 것이고 \(\vec{u}\)로 \(\perp\)하게 수선의 발을 내리자! 그렇게 되면 그 길이는 오차다
자 여기서 각x,y 점들의 분포의 분산을 가장 잘 설명하는 방향은 projection 내렸을 때 \(error^2\)을 가장 작게 만드는 방향으로 향하더라

아래 영상을 보면 최소 구간을 찾다가 찾으면 멈춰서 말 그대로 수선의 발을 내려 \(\perp\)된다

아 이것으로 1️⃣ 왜 분산이 가장 큰 방향이 이 분포를 잘 설명하는가? 에 대한 질문은 해결이 되었군
이어서 min을 구하는데 필요한 수선의발 즉 error의 길이를 구하기 위해 아래 표를 보자

----------------참고-------------------
(1) \(d_i^T u\)   정사영한 결과 \(\Rightarrow\) 즉 스칼라
(2) \(d_i^T u\cdot u\)   정사영한 결과에 u와 내적하여 u방향성분을 획득
(3) \(\left(d_i-d_i^T u\cdot u\right)\)   \(d_i\) 벡터에서 u벡터의 성분 제거
(즉 \(a^Ta\) 꼴로 만들면 제곱처럼 되어 높이인 오차를 구할 수 있다)
-------------------------------------------

자 저 데이터 하나의 error length에 대한 식은 이렇다 \(\color{red}{\Rightarrow}\) \(\left(d_i-d_i^T uu\right)^T \left(d_i-d_i^T uu\right)\)
어 이건 \(L_2\) norm의 \(\sqrt{x_1^{2}+x_2^{2}+\cdots}\) 형식이네?

근데 아까도 말했지만 \(d_i\)들 중 한 점이 아니라 N개의 모든 데이터에서 고려해야하니
\(\frac{1}{N}\sum_{i} \left(d_i-d_i^T uu\right)^T \left(d_i-d_i^T uu\right)\\ S.T. \quad \vert\vert u\vert\vert_2^2 = u^Tu=1\)
해석 \(\Rightarrow\) 전체 \(d_i\) error length를 더한 것을 제곱해 N개로 나눠주는데,   조건은 오차거리제곱이 1일것

여기서 분배법칙해보자    참고로 \(d_i^T u\)는 스칼라라서 transposed 영향 안 받는다
\(\frac{1}{N}\sum_{i} \left(d_i^Td_i-d_i^Tu\cdot u^Td_i-d_i^T(d_i^Tu)u+d_i^Tu\cdot u^T(d_i^Tu)u\right)\)
자 아까 임의로 $u^Tu=1$로 조건을 부여하였고 스칼라는 앞으로 보낼 수 있으니까
\(\frac{1}{N}\sum_{i} \left(d_i^Td_i-d_i^Tu\cdot u^Td_i-(d_i^Tu)d_i^Tu+(d_i^Tu)d_i^Tu\cdot u^Tu\right)\\ \Rightarrow \frac{1}{N}\sum_{i} \left(d_i^Td_i-d_i^Tu\cdot u^Td_i\right)\)
위처럼 전개가 되는데 우리는 \(\vec{u}\)가 필요하고, \(d_i^Td_i\) 이거 필요 없으니까 제거하자
why?–> 어차피 데이터의 제곱합을 구할건데 저건 bias라서 있으면 모델 예측에 불필요한 영향을 주거든

그렇게 되면 남는 식은 아래와 같다
\(\Rightarrow \frac{1}{N}\sum \left(-d_i^Tu\cdot u^Td_i\right)\)
자 그리고 아까 error인 이식을 참고 하자   \(d_i=\tilde{d_i}-\bar{d_i}\)
그리고 u는 \(d_i\)와 관계없으니 앞에 빼주자 그럼 식을 위치를 바꾸어 전개 가능하겠네⬇️
\(\Rightarrow \frac{1}{N}\sum_{i} \left(-u^Td_i\cdot d_i^Tu\right) \\ \Rightarrow -u^T\frac{1}{N}\sum \left(d_i\cdot d_i^T\right)u \\ \Rightarrow -u^T\frac{1}{N}\sum_i \left((\tilde{d_i}-\bar{d_i})(\tilde{d_i}-\bar{d_i})^T\right)u\)

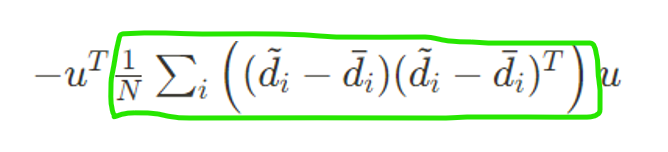
자 \(\color{lightgreen}{\square}\)는 sample covariance matrix랑 비슷하네?
\(\begin{bmatrix} cov(x,x) & cos(x,y) \\cov(y,x) & cos(y,y) \end{bmatrix}\)   이게 covariance matrix인데 symmetric하여 diagonalizable하기 때문이다.
근데 diagonalizable하다고 symmetric하지는 않다 알아두자
아무튼 \(\color{lightgreen}{\square} = R_d\)라 하겠다
자 그러면 \(-u^TR_du\)라고 표현할 수 있겠네
이때 \(R_d\)를 통해 생각할 수 있는 것들    \(\begin{cases}if \quad 1D \rightarrow 분산\\ if \quad 2D \rightarrow covariance \quad matrix\end{cases}\)

자 요약하자면 \(min=-u^T\frac{1}{N}\sum_i \left((\tilde{d_i}-\bar{d_i})(\tilde{d_i}-\bar{d_i})^T\right)u\) 이고
변수를 통해 바꾸면 \(min\color{red}{=}-u^TR_du\) 이렇게 표현할 수 있겠네

(2) 🧏‍♀️maximize(최대화)

자 간단하게 얘기해 위의 식에서 -부호만 뺀 것이다   \(max\color{red}{=}u^TR_du\)
이것에 대한 증명은 Lagrangian function 쓰자
\(L=u^TR_du+\gamma(1-u^Tu)\)

\(\vec{u}\) 에 대한 미분 \(\Rightarrow\) 즉 \(\vec{u}\)에 대한 변화량을 알아본다는 뜻이다.
\(dLu=du^TR_du\color{red}{+} u^TR_ddu\color{red}{-}\gamma d\color{skyblue}{u^Tu}\color{red}{-} \gamma\color{skyblue}{u^T}d\color{skyblue}{u}\)
여기서 \(\color{skyblue}{u^Tu}\)는 스칼라니까 transposed 취해도 똑같다

\(\Rightarrow 2u^TR_du \color{red}{-} 2\gamma u^Tdu \\ = \color{violet}{(}2u^TR_d-2\gamma u^T\color{violet}{)}du\)
이식에서 $\color{violet}{(}~~~~\color{violet}{)}$ 부분은 $\frac{dL}{du^T}$다 이게 무슨말이냐면 L/ u row vectors로 미분했다는 뜻

---------------벡터의 미분-----------------
1개씩 미분한 것을 가로로 쌓은 것
\(\frac{dL}{du^T}\) \(\color{red}{=}\) \(\left[\frac{dL}{du_1} \color{lightgreen}{,} \frac{dL}{du_2} \color{lightgreen}{,} \frac{dL}{du_3} \cdots\right]\)
---------------------------------------------

아무튼 우리는 \(\color{violet}{(}~~~~ \color{violet}{)}\)du 라는 식에서 \(\color{violet}{(}~~~~ \color{violet}{)}\)가 미분이란 것을 알 수 있다

🧑‍🎨계산

자 그럼 우리가 할 것은 $\frac{dL}{du^T}=0$ 을 만족하는 u 중에서 가장 max를 찾아야 하고 아까 $L$식을 만족한다
아무튼 아까 \(\color{violet}{(}~~~~\color{violet}{)}\)식에서 양변으로 넘기면 \(u^Tr_d=\gamma u^T\)가 되네
그리고 transposed 취해주자 why—> \(R_d\)가 symmetric하니 당연히 diagonalizable하여 orthogonal matrix로 decompose 가능
(참고로 \(\gamma\)는 스칼라라 transposed 영향 없다)

\(\left(u^Tr_d\right)^T=\left(\gamma u^T\right)^T \\ \color{red}{\Rightarrow} R_du = \gamma u \quad\quad\quad (\gamma: EigenValue,\quad u: EigenVector)\)

자 이제 \(R_d\)를 decompose 하자
그러기 위해 아까 전에 봤던 식인 \(max=u^TR_du\)로 넘어가자
\(R_d\):     symmetric해서 diagonalizable되므로 orthogonal matrix로 decompose된다고 했다
\(u^TR_du \color{red}{=} u^T\left(\gamma_1 q_1q_1^T \color{red}{+} \gamma_2 q_2q_2^T \color{red}{+} \cdots \right)u\)
u가 무엇일 때 \(q_1, ~~ q_2, ~~ \cdots\)가 큰 값으로 나올까 ?

자 아까 u는 \(R_d\)의 EigenVector라고 했다 그말은 u가 \(q_1, q_2, \cdots\) 중에 하나라는 얘기다
좋다 그럼 만약 \(\gamma_1 \quad \gamma_2\cdots\)이 내림차순이고,   \(u=q_1\) 로 보자
\(\Rightarrow q_1^T \left(\gamma_1 q_1q_1^T\right)q_1\)   이렇게 되는데 \(q_1^Tq_1=1\)로 상쇄되니 \(\gamma_1\)만 남는다
자 그럼 내림차순이라 했으니 \(\gamma_1\)이 가장 큰 주성분 벡터고 그다음으로는 \(\gamma_2\)다
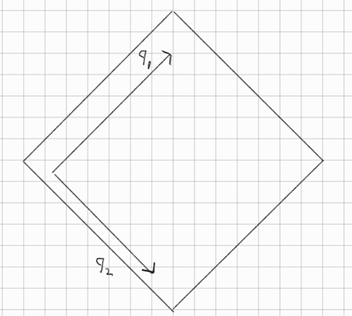
참 \(q_1 \perp q_2\)니까 즉 orthogonal하여 아래 그림의 분산정도를 보면 \(q_2\)가 왜 2번째로 큰 주성분으로 분포를 잘 설명하는지 알 수 있다

자 이제 2️⃣ 왜 그다음으로 잘 설명하는 방향은 첫 번째 주성분에 수직하냐? 질문에 대한 답을 할 수 있다

3. PCA 응용

3-1. 차원축소(예시)

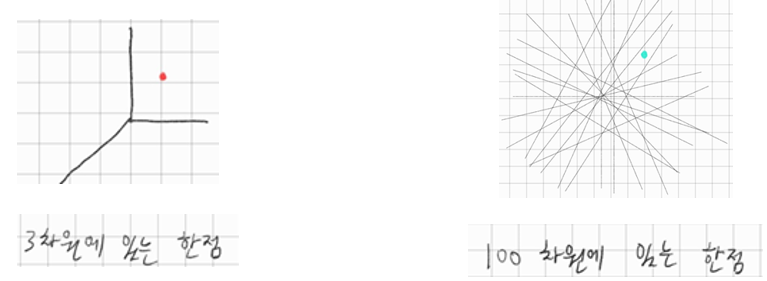
100차원 데이터가 있다고 가정하자

\(\begin{bmatrix} x\\y\\z\\ \vdots\\\vdots\\\vdots \end{bmatrix}\)   이것을 100차원의 한 점이라 하자

여기서 100 Dim data에 있는 한 점 —> 2 Dim data로 축소하려면
i번째 데이터가 있을 때 축소한 결과가 이렇게 된다 \(d_i^Tq_1\cdot q_1+d_i^Tq_2\cdot q_2\)
자 앞에서도 얘기했지만 바로 위의 식은 각각 (내적x방향성) + (내적x방향성)을 나타낸 거이다
아무튼 이 식이 무슨 말이냐면 어떤 공간이 있을 때 2 Dim에 내린다는 것인데
이 2차원은 \(q_1 \quad q_2\)가 span 하는 곳이다

이게 무슨 말이냐면 \(q_1=\begin{bmatrix} \vdots\\\vdots\\\vdots \end{bmatrix}, \quad q_2=\begin{bmatrix} \vdots\\\vdots\\\vdots \end{bmatrix}\)   각각 100개의 데이터가 있는데
\(q_1\)과 \(q_2\)로 linear combination 즉 span하게 되면
\(a\begin{bmatrix} \vdots\\\vdots\\\vdots \end{bmatrix}+ b\begin{bmatrix} \vdots\\\vdots\\\vdots \end{bmatrix}\)   즉 2 Dim 평면만 나타낸다는 뜻

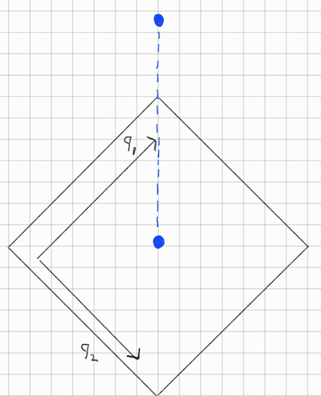
자 그럼 \(\color{blue}{\bullet}\)을 100 Dim 위의 한 점이라 하고 그것을 아래로 내렸다고 치자

여기서 2 Dim으로 내린 점이 \(d_i^Tq_1\cdot q_1+d_i^Tq_2\cdot q_2\) 다

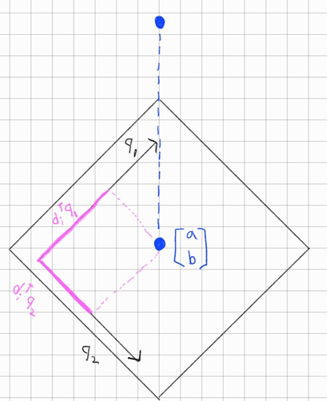
자 여기서 정사영한 점의 값을 찾기 위해 좌표값을 구해야되는데
\(q_1\) 축으로의 좌표값을 내적한 값 \(\Rightarrow\) \(d_i^Tq_1\)
마찬가지로 $q_2$ 축으로의 좌표값을 내적한 값 \(\Rightarrow\) \(d_i^Tq_2\)
그럼 정사영한 점을 표현하려면 \(a\begin{bmatrix} 1\\0 \end{bmatrix}+ b\begin{bmatrix} 0\\1 \end{bmatrix}\)   이런식으로 진행되겠지?

정사영한 점의 식은 아래 식의 역할을 대체해준다

음 그러면 데이터 10000개 중에서 \(q_{1(100*1)}\),   \(q_{2(100*1)}\)이니
2차원 축소를 위해서는 숫자 200개가 필요하겠군

3-2. 차원축소(영상)

16x16인 256 Dim에서 PCA를 통해 3 Dim으로 압축했을 때

참고

1. 혁펜하임    주성분 분석 (PCA: Principal Component Analysis) 의 모든 것!, 고윳값 분해의 응용
2. 공돌이의 수학정리 노트     주성분 분석(PCA)의 기하학적 의미
3. 브릭     주성분 분석 (PCA)의 원리와 전사체 데이터 분석에서의 활용
4. 고려대학교 산업경영공학부 DSBA     01-4: Dimensionality Reduction - PCA