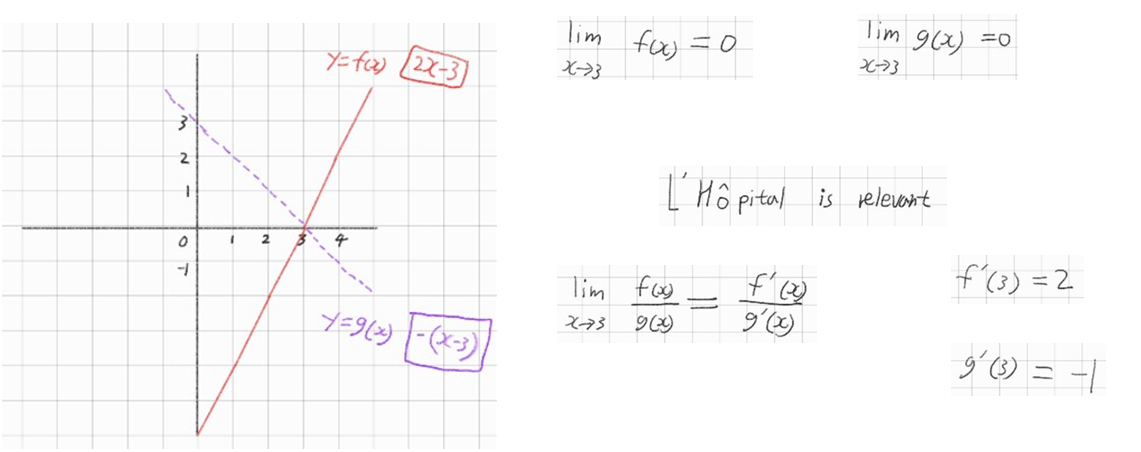롤의 정리 & 평균값 정리 & 로피탈 정리
🙅♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다
1
2
3
4
5
6
<목차>
1. PreRequisites
2. 롤의 정리
3. 평균값 정리
4. L'hopital's theorem
1. PreRequisites
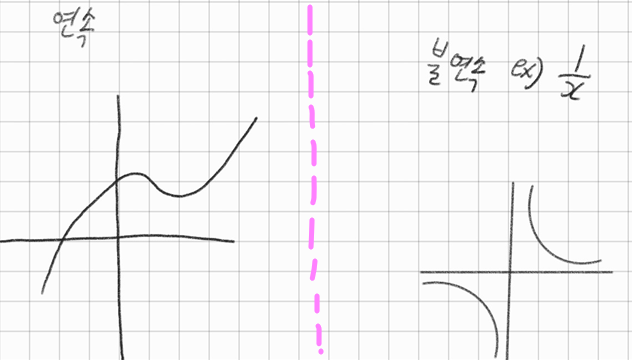
1-1. 연속함수 vs 불연속함수
말그대로 쭉 연결되는 함수 vs 가다가 중간에 끊기는 함수다
참고로 \(\bullet\)은 이어지는(닫힌), \(\circ\)는 열린(연속이 아닌)이다
자 그러면 함수가 연속일 조건은? 3가지다
(1) 함수 f(x)에 대해 x=a에서 함숫값 f(a)가 존재해야 한다
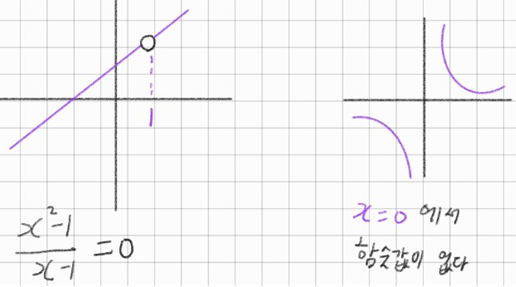
우선 이 그래프들은 (밑줄) 2개 다 불연속이다
왼쪽 그래프를 보면 x에 1이 들어가면 분모가 0이 되기에 연속이 안되서 약분하여
\(x+1\) 을 만들고 싶다면 그때의 조건은 \((x \neq 1)\) 이다
그리하여 그래프가 가다가 1에서 함숫값이 없다(끊어졌다)
\(\therefore x=1\) 에서는 함숫값이 존재하지 않는다
우측 그래프를 보면 \(x=0\) 일때, 함수값이 없다
(2) x=a에서 극한값 존재(\(\lim_{x\to a}f(x)\)가 존재)
즉 좌극한, 우극한이 존재해야하고 또 같아야 한다. 이를 나타내면 아래와 같다
\(\lim_{x\to a^-}f(x) \quad = \quad \lim_{x\to a^+}f(x)\)
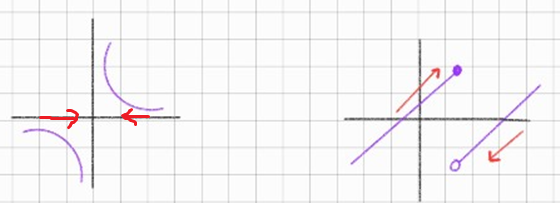
좌측 그래프를 보면 \(x=0\) 에서 함숫값도 없고, 극한값도 없다
왜? a가 0보다 큰쪽에서 다가갈 때 발산하고 a가 0보다 작은쪽에서 다가갈때도 발산하니까
즉 \(x=0\) 에서 불연속이다
우측 그래프는 아래의 구간에 따라 2개의 함수로 정의된 것이다
\(f(x) = \begin{cases} x+1 \quad (x \leq1)\\ x-2 \quad (x >1)\end{cases}\)
극한값이 존재하려면 좌극한=우극한 이어야하는데 그래프에서는 그렇지 않다.
그러므로 극한값이 존재하지 않아 불연속.
(3) 함숫값 = 극한값 일 것
즉, \(f(a) = \lim_{x\to a} f(x)\) 이 되야 한다
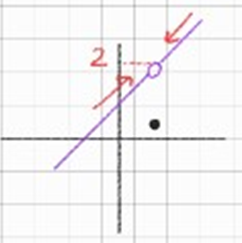
위 그래프는 아래와 같다
\(f(x) = \begin{cases} \frac{x^2-1}{x-1} \quad (x \neq 1)\\ 1 \quad\quad (x=1)\end{cases}\)
음 \(f(1)=1\)이네 위에 보면 \(\bullet\) 표시
좌극한, 우극한 값도 각각 2라서 극한값 2로 존재하네
\(\lim_{x\to 1^-} f(x) = 2 \quad\quad\quad \lim_{x\to 1^-} f(x) = 2 \quad\quad \therefore \lim_{x\to 1} f(x) = 2\)
근데 함숫값 \(\neq\) 극한값 이라 불연속이다
즉 함수의 연속을 만족하려면 위의 3가지 조건을 만족해야 한다 (반드시 암기)
1-2. 닫힌구간 vs 열린구간
구간 \(x\)에서 닫힌구간은 [], 열린구간은 () 표시한다.
닫힌구간: \([a,b] \rightarrow a \leq x \leq b\)
열린구간(개구간) : \((a, b) \rightarrow a < x < b\)
2. 롤의 정리
함수 \(f(x)\)가 폐구간 $[a, b]$에서 연속이고 개구간 (a,b)에서 미분가능할 때
\(f(a)=f(b)\)면 \(f'(c)= 0\) 즉 (a < c < b)를 만족시키는 c가 적어도 하나 존재한다
즉 쉽게 말해
- 구간 양끝점의 함숫값이 같고,
- 그 구간사이가 연속이고
- 항상 그 구간에서 미분 가능하면
a~b 사이의 어떤 값에서 미분계수값이 0이 되는 값이 적어도 1개 이상은 존재한다라는 뜻
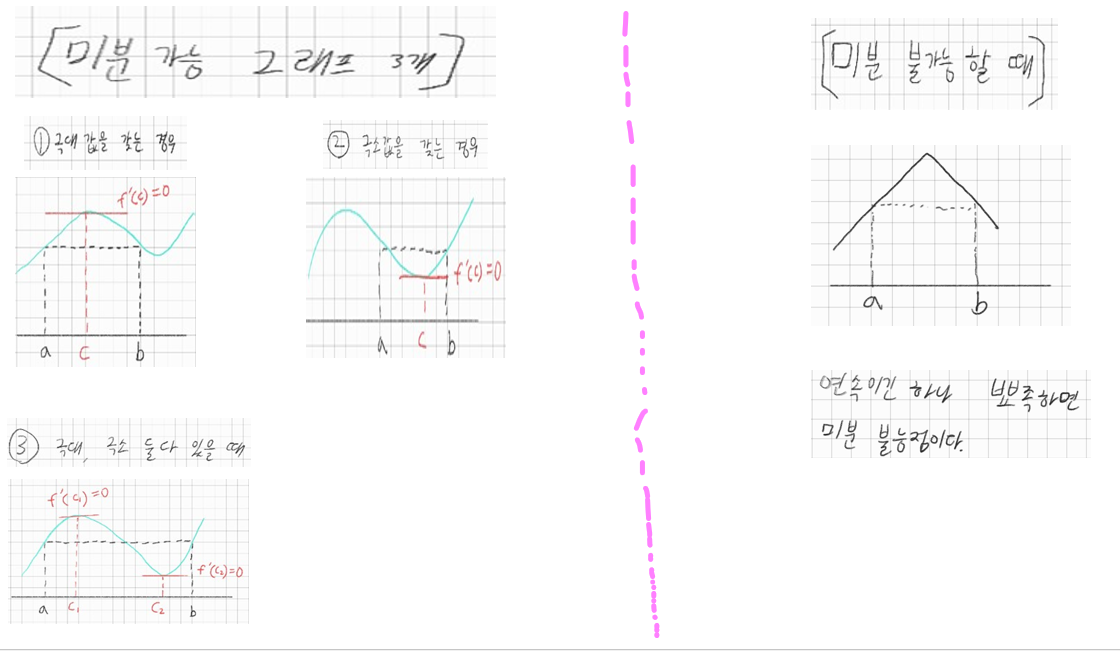
여기서 2가지 경우를 살펴볼 수 있다
case 1)
[a, b]에서 f(x)가 상수이면 모든 점에서 \(f'(x)=0\) 이므로 \(f'(c)=0\)을 만족시키는 점 c( a< c < b)가 적어도 하나 존재한다
case 2)
f(x)가 상수함수가 아니면 \(f(x_0) \neq f(a) \quad\quad (\because f(a)=f(b))\)인 점 \(x_0 \quad (a<x_0<b)\)가 존재한다.
또 최대최소 theorem에 의해 f는 [a, b]에서 최댓값과 최솟값을 가진다
그런데 f(a)=f(b)이므로 어떤 점 c(a < c < b)에서 최댓값 f(c)를 가지면 f(c)는 극댓값이고 페르마 정리에 의해 \(f'(c)=0\)이다
또 어떤 점 c(a < c < b)에서 최소값 f(c)를 가지면 f(c)는 극솟값이고 페르마 정리에 의해 \(f'(c)=0\)이다
3. 평균값 정리
우선 roll’s theorm처럼 양끝의 함숫값이 같을 필요는 없고,
함수 f(x)가 폐구간 [a, b]에서 연속이고 개구간 (a, b)에서 미분 가능하면
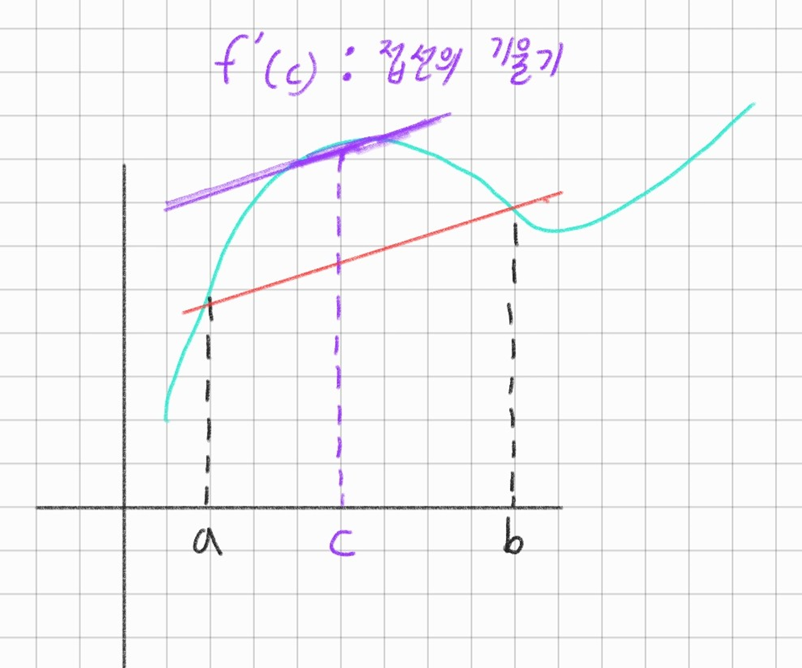
\(\frac{f(b)-f(a)}{b-a} = f'(c) \quad\quad (a < c < b)\) 를 만족하는 c가 적어도 하나 이상 존재한다
즉 좌측에 보이는 평균변화율 값을 갖는 이 미분 계수값이 적어도 a와 b 사이에 적어도 1개 이상 있다는 말이다
참고로 위의 그림에서 보라색 선은 바로 아래 직선과 평행한 c에서 그은 접선이다
평균값의 정리에 대해 조금 더 부연설명을 해보겠다
\(F(x) = f(x)-f(a)-\frac{f(b)-f(a)}{b-a}(x-a)\)라 두면
\(F(x)\)는 [a, b]에서 연속이고 (a, b)에서 미분가능이며 F(a)=F(b) (=0)이므로 롤의 정리에 의해 \(F'(c)=0$인 $c(a < c < b)\)가 적어도 하나 존재한다.
그런데 \(F'(x) = f'(x)-\frac{f(b)-f(a)}{b-a}\) 이므로 결국 \(F'(c)=f'(c)-\frac{f(b)-f(a)}{b-a}=0\)
즉 \(\frac{f(b)-f(a)}{b-a}=f'(c) \quad\quad (a<c<b)\)를 만족하는 c가 적어도 1개 이상 존재한다
예제-1(평균값 정리)
모든 실수 \(x\)에 대하여 미분가능한 함수 f(x)가 \(\lim_{x\to \infty} f'(x)=4\) 를 만족할 떄
\(\lim_{x\to \infty} \left\{ f(x+2) - f(x-2) \right\}\) 의 값을 구하여라
sol
f(x)는
- 폐구간 [x-2, x+2]에서 연속이고
- 개구간 (x-2, x+2)에서 미분가능하므로
평균값 정리에 의해 \(\frac{f(x+2)-f(x-2)}{(x+2)-(x-2)}= f'(c) \quad\quad (x-2 < c < x+2)\)
여기서 식을 이렇게 고칠 수 있다 \({f(x+2)-f(x-2)}= 4f'(c)\)
어? 잠깐
여기서 \(x-2\to \infty\), \(x+2\to \infty\) 라면 c도 자연스럽게 무한대로 간다
그러면 이렇게 도출되네? \(\lim_{c \to \infty} 4f'(x)=?\)
\(\lim_{c \to \infty} f'(x) \quad = \quad \lim_{x \to \infty} f'(x)\) 이므로 답은 16이다
예제-2(평균값 정리)
\(\lim_{x \to 0^+} \frac{e^x-e^{sinx}}{x-sinx}\) 의 값을 평균값의 정리를 이용하여 구하시오
sol
\(f(x)=e^x\) 라 두면 f(x)는 \(\forall x\)에서 미분 가능하다 \(\color{red}{\Rightarrow}\) 평균값 정리 성립
\(x \to 0^+\) 면 \(c \to 0^+\) 도 맞다
즉 \(x \to 0^+\) 면 \(sinx \to 0^+\)도 맞다는 것이다
\(sinx\) 극한에 관해 아래 그래프를 보자
\(x\)가 한없이 0보다 큰 곳에서 접근하면 sin 함수값도 0보다 큰 곳에서 접근한다
\(\therefore \lim_{c \to 0^+} f'(c) = \lim_{c \to 0^+} e^c = e^0 =1\) 이다
4. L’hopital’s theorem
함수 \(f\)와 \(g\)가 \(\forall x\)에 대해 미분 가능하고 \(x=a\) 근방에서 \(g'(a) \neq 0\) 이라 하자
그러면 \(\lim_{x \to a} f(x)=0\) 이고 \(\lim_{x \to a} g(x)=0\)
(또 \(\lim_{x \to a} f(x) \pm \infty\) 이고 \(\lim_{x \to a} g(x) \pm \infty\) ) 이고
\(\lim_{x \to a} \frac{f'(x)}{g'(x)}\)가 존재하면, \(\lim_{x \to a} \frac{f(x)}{g(x)}= \lim_{x \to a} \frac{f'(x)}{g'(x)}\) 다.
\(\frac{0}{0} (0분의 0)\) 혹은 \(\frac{\infty}{\infty}\)도 가능하다는 말이다
아래 그래프 예시를 보자
로피탈 정리 예제
(1) \(\lim_{x \to \frac{\pi}{2}} (secx-tanx)\)
sol: 식을 고치면 아래와 같다
\(\lim_{x \to \frac{\pi}{2}} \left( \frac{1-sinx}{cosx} \right)\)
x에 \(\frac{\pi}{2}\)을 대입했을 때 \(\frac{0}{0}\)이기에 로피탈 정리를 사용할 수 있다고 판단
\(\Rightarrow^{(L \cdot H)} \lim_{x \to \frac{\pi}{2}} \frac{-cosx}{-sinx}\) 이는 결국 \(\frac{0}{-1}\)으로 수렴하기에 0이 된다
(2) $\lim_{x \to 0^+} (sinx)^x$
sol:
우선 \(y=x^x\) 꼴이네? 이건 조금 복잡해서 로그의 미분규칙을 이용해 풀어야 한다
- 양변에 로그 곱하기 \(ln_ey= ln_ex^x \quad \Rightarrow ln_ey =xln_ex\)
- \(\frac{d(lny)}{dx} = lnx+1\) (참 lnx 미분하면 \(\frac{1}{x}\)임)
- 위의 식을 이렇게도 표현 가능하겠다? \(\frac{d(lny)}{dy} \cdot \frac{dy}{dx} = lnx+1\)
\(\Rightarrow\) \(\frac{dy}{dx} = y \cdot (lnx+1)\) \(\therefore \quad \frac{dy}{dx}= x^x \cdot (lnx+1)\)
자 그러면 위의 방법을 참고하면 \(ln(sinx)^x = xln(sinx)\)로 고칠 수 있겠지?
자 그러면 로그변환한 극한 확인하자
\(\lim_{x \to 0^+} ln(sinx)^x\) 이걸 이렇게 고칠 수도 있다 \(\lim_{x \to 0^+} \frac{ln(sinx)}{\frac{1}{x}}\)
참 \(ln0 \to -\infty\) 다 why? —> 진수가 한없이 작아지면 로그 전체값은 한없이 -음수로 감
자 위의 식에 0을 넣어보니 \(\lim_{x \to 0^+} \frac{ln0}{\frac{1}{0}} = \frac{-\infty}{\infty}\) 꼴이 되네?
그러면 L'hopital's Rule 이 적용 가능하다
\(\lim_{x \to 0^+} \frac{ln(sinx)}{\frac{1}{x}}\)에서 \(L\cdot H\) 적용 (pink) \(\Rightarrow\) \(\lim_{x \to 0^+} \frac{\frac{cosx}{sinx}}{\frac{-1}{x^2}}\)
이 식에 대해 x를 각각 배치해보자 → \(\lim_{x \to 0^+} \left( -x \cdot cosx \right) \frac{x}{sinx}\)
각 x에 0을 넣으면 \((-0 \cdot 1) \cdot 1 =0\) 이 된다.
여기서 지금 \(\lim_{x \to 0^+} ln \Delta = 0\) 꼴인데 좌측의 ln을 없애면 \(\Rightarrow \Delta = e^0\) 즉 1
마무리:
좋다. \(\lim_{x \to 0^+} ln(sinx)^x =0\) 을 만족하려면
\(\lim_{x \to 0^+} (sinx)^x=1\) 을 만족해야겠지?
\(\therefore\) 정답은 1