삼각함수의 덧셈정리
🙅♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다
1
2
3
4
5
6
7
<목차>
1. 삼각함수의 덧셈정리 공식
1-1 (1)의 증명
1-2 (2)의 증명
1-3 (3)의 증명
1-4 각 3개일 때
2. 예제
preRequisites
- 원점에서의 sin, cos 좌표의 의미
- 짤막한 팁 $\Rightarrow$ $tan \theta = \frac{sin \theta}{cos \theta}$
- 삼각함수의 역수⬇️
\(\begin{cases} csc \theta = \frac{1}{sin \theta} \\ sec\theta = \frac{1}{cos\theta} \\ cot\theta = \frac{1}{tan\theta} \end{cases}\)
1. 삼각함수의 덧셈정리 공식
(1) \(sin(\alpha + \beta) = sin \alpha \cdot cos \beta + cos \alpha \cdot sin \beta\)
\(\quad sin(\alpha - \beta) = sin \alpha \cdot cos \beta - cos \alpha \cdot sin \beta\)
(2) \(cos(\alpha + \beta) = cos \alpha cos \beta - sin \alpha sin\beta\)
\(\quad cos(\alpha - \beta) = cos \alpha cos \beta + sin \alpha sin\beta\)
(3) \(tan(\alpha + \beta) = \frac{tan \alpha + tan \beta}{1-tan \alpha \cdot tan \beta}\)
(4) \(tan(\alpha - \beta) = \frac{tan \alpha - tan \beta}{1+tan \alpha \cdot tan \beta}\)
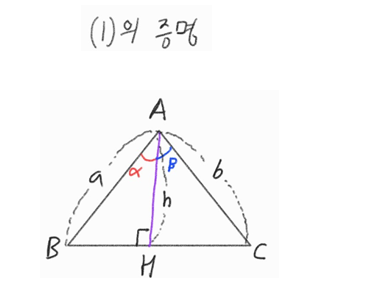
\(\Delta\) ABC 넓이 = \(\Delta\) ABH 넓이 + \(\Delta\) ACH 넓이
\(\Rightarrow\) \(\frac{1}{2}ab sin (\alpha + \beta) = \frac{1}{2}ah sin \alpha + \frac{1}{2}bh sin \beta\)
\(\Rightarrow\) \(sin (\alpha + \beta) = \frac{h}{b}sin \alpha + \frac{h}{a} sin \beta\)
아 삼각형을 보니 아래처럼 식을 고칠 수도 있겠네
\(\Rightarrow\) \(sin (\alpha + \beta) = cos \beta \sin \alpha + cos \alpha sin \beta\)
\(\therefore\) \(sin \alpha \cdot cos \beta + cos \alpha \cdot sin \beta = sin(\alpha + \beta)\)
★어 잠깐! \(sin(-\theta) = -sin\theta\)
\(cos(-\theta) = cos\theta\)
\(tan(-\theta) = -tan \theta\)
이걸 보니 (1)증명으로부터
\(\quad sin(\alpha - \beta) = sin \alpha \cdot cos \beta - cos \alpha \cdot sin \beta\) 이 식도 자연스럽게 유도되지 않는가?
이것을 보니 제 2코사인 정리를 이용하면 되겠네 아래 삼각형을 참고하자
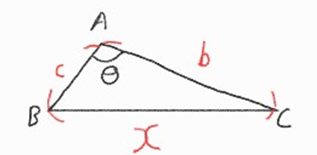
제 2코사인 정리: $x^2 = b^2 + c^2 -2bc \cdot cos\theta$
이제 다시 원으로 돌아가서 증명해보자
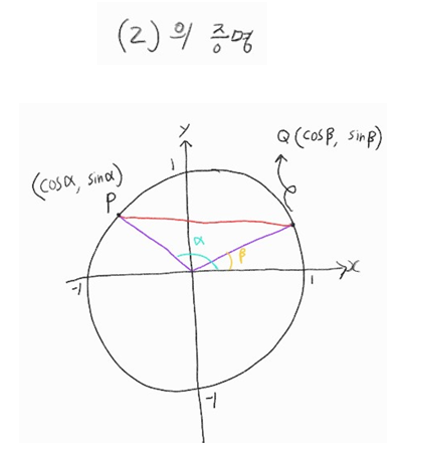
우선 보니 사잇각이 \(\alpha - \beta\), 그리고 보라색 선에서 각각 P, Q까지의 거리가 1이네?
\(\overline{PQ}^2 = 1^2 + 1^2 -2 cos(\alpha-\beta)\) 이 식을 ㄱ이라 하겠다
위의 코사인 제2 법칙 외에, 이번에는 두 점사이의 거리 공식을 이용하면 되겠다
\(\overline{PQ}^2 = cos(\alpha-\beta)^2 + sin(\alpha-\beta)^2\)
여기서 $sin^2 \theta + cos^2 \theta = 1$ 인 것은 알고 있겠지?
\(\overline{PQ}^2 = 1+1-2(cos\alpha \cdot cos\beta - sin \alpha \cdot sin\beta)\) 이 식은 ㄴ이라 하겠다
아 ㄱ=ㄴ 이네? 약분하고 고치면 \(\overline{PQ}^2 = cos \alpha cos \beta + sin \alpha sin\beta\) 됨
여기서 만약에 \(\beta\) 대신에 \(-\beta\)를 넣으면 \(cos \alpha cos \beta - sin \alpha sin\beta\)가 되므로
$cos(\alpha + \beta)$가 된다
(3)의 증명
\(tan \theta = \frac{sin \theta}{cos \theta}\) 를 이용해보자
그러면 \(tan (\alpha + \beta) = \frac{sin (\alpha + \beta)}{cos (\alpha + \beta)}\) 라고 고칠 수 있겠네
위의 식을 삼각함수 덧셈법칙을 이용하여 전개해보자
\(tan (\alpha + \beta) = \frac{sin (\alpha + \beta)}{cos (\alpha + \beta)}\)
\(\quad\quad\quad\quad\quad = \frac{sin \alpha \cdot cos \beta + cos \alpha \cdot sin \beta}{cos \alpha cos \beta - sin \alpha sin\beta}\)
여기서 분자, 분모를 \(\div cos \alpha cos \beta\) 하면
\(\begin{align*} &=\frac{\frac{\sin \alpha}{\cos \alpha} + \frac{\sin \beta}{\cos \beta}}{1 - \frac{\sin \alpha}{\cos \alpha} \cdot \frac{\sin \beta}{\cos \beta}} \\ &= \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \cdot \tan \beta} \\ &\Rightarrow \tan(\alpha + \beta) \end{align*}\)
😎만약에 tan 각도 3개짜리면 어떻게 하지?
\(tan (\alpha + \beta+ \gamma) \Rightarrow tan (\theta+ \gamma)\)
위처럼 \(\alpha + \beta\)를 \(\theta\)로 치환하여 진행하면 된다
2. 예제 2개
2-1 예제1
좌표평면에서 $\alpha + \beta = \gamma$ 일 때, 점 $P$의 $y$좌표는?
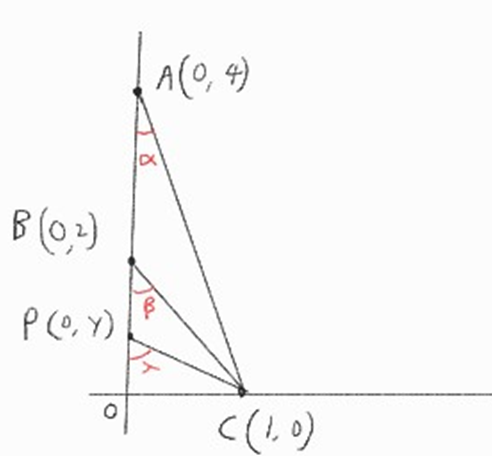
sol:
문제에서 제시한 \(\alpha + \beta = \gamma\)을 우선 생각하고 시작하자
\(\Delta POC\)에서 \(y\)를 보니 \(tan(\gamma) = \frac{1}{y}\) 이네, 그럼 \(\Rightarrow y= \frac{1}{tan(\gamma)}\)
어?? 가만 보니 \(tan(\alpha+\beta)\)를 통해 구할 수 있겠다
\(tan(\alpha) = \frac{1}{4}\), \(tan(\beta) = \frac{1}{2}\)
자 그럼 \(tan(\alpha+\beta) = \frac{tan\alpha + tan\beta}{1-tan\alpha \cdot tan\beta} = \frac{\frac{1}{4} + \frac{1}{2}}{1- \frac{1}{4} \cdot \frac{1}{2}} = \frac{6}{7}\)
즉 P좌표는 \((0, \frac{6}{7})\)이 되어 y는 \(\frac{6}{7}\) 이다
2-2. 예제2
\(\begin{cases} sin \alpha + sin \beta + sin \gamma = 0 \\ cos \alpha + cos \beta + cos \gamma = 0 \end{cases}\) 일 때, \(cos(\alpha - \beta)\)의 값을 구하시오.
sol:
\(\begin{cases} (sin \alpha + sin \beta)^2 = (-sin \gamma)^2 \\ (cos \alpha + cos \beta)^2 = (-cos \gamma)^2 \end{cases}\) 이렇게 변형시켜
위의 식과 아래식을 더하면 대충 A+B=1 꼴로 나오는데 여기서 \(cos(\alpha - \beta)\)랑 같다고 표시하면 풀 수 있다
\(\therefore\) 답은 \(-\frac{1}{2}\)가 나온다
2-3. 예제3
\(A+B+C=90^\circ\) 일 때,
\(tan(A)tan(B)+ tan(B)tan(C)+tan(C)tan(A)\)를 구하여라
sol:
\(A+B=90^\circ-C\) \(\color{red}{\Rightarrow}\) \(tan(A+B) = tan(90^\circ-C) = cot(C)\)
참고로 \(cot(C) = \frac{1}{tan(C)}\)
\(\Rightarrow\) \(\frac{tan(A) + tan(B)}{1-tan(A) \cdot tan(B)} = \frac{1}{tan(C)}\)
여기서 계산하면 ㅁ=1 이런 꼴로 나온다
만약 각각 A,B,C가 \(30^\circ\)라 하면 \(\frac{1}{\sqrt3} \frac{1}{\sqrt3} + \frac{1}{\sqrt3} \frac{1}{\sqrt3} + \frac{1}{\sqrt3} \frac{1}{\sqrt3} =1\) 마찬가지로 성립하는게 보인다

