visualizing complex vector based on euler’s formular

🙅‍♂️휴대폰으로 볼 때 혹시 글자나 숫자가 화면에 다 안나오면, 휴대폰 가로로 돌리시면 됩니다

<목차>

1. 들어가며 
2. 회전행렬의 고윳값, 고유벡터
3. 복소수와 오일러공식 
4. 회전변환과 고유벡터의 상호작용

1. 들어가며

이번시간에는 회전행렬의 고윳값과 고유벡터가 오일러의 공식과 어떤 연관이 있는지 알아볼 것입니다.

Prerequisites

• 자연상수(e)의 의미
  
• 고윳값, 고유벡터
  
• 복소벡터
  
• 오일러 공식의 기하학적 의미
  
  
  
  

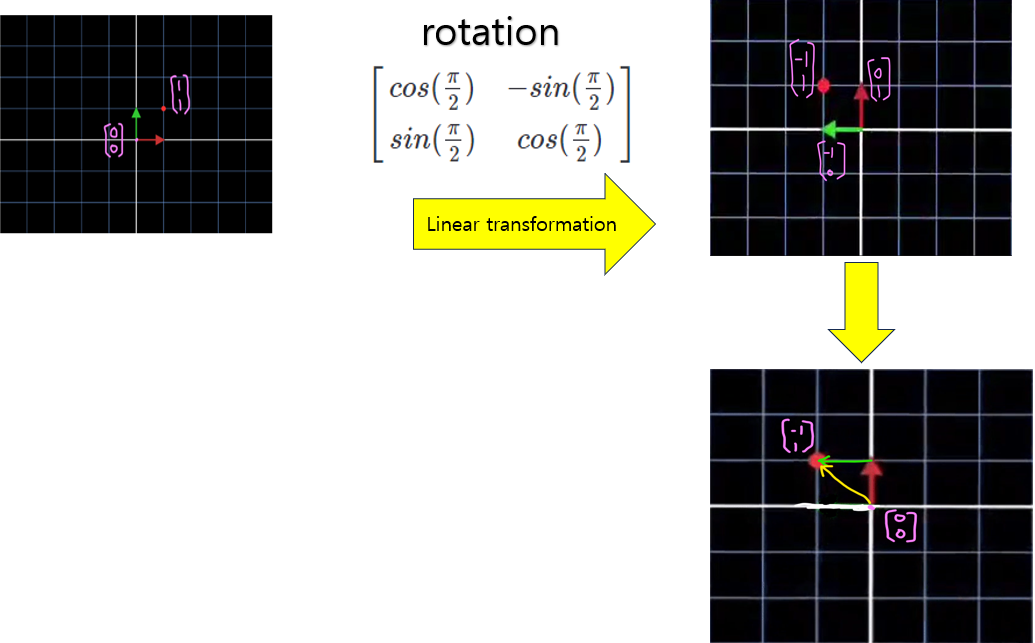
2. 회전행렬의 고윳값, 고유벡터

🎲회전행렬의 고윳값 계산

\(A\vec{x} = \gamma \vec{x} \\ \begin{bmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{bmatrix} \vec{x} = \gamma \vec{x}\)

$(A-\gamma I_2)\vec{x} = 0$

참고로 위의 행렬을 B라 하면 역행렬인 \(B^{-1}\)을 가지면 안됨
\(det \left( \gamma I_2 -A \right) \\ \rightarrow det\begin{pmatrix} cos \theta-\gamma & -sin \theta \\ sin \theta & cos \theta-\gamma \end{pmatrix} = 0 \\ \rightarrow (cos \theta-\gamma)^2 + sin^2\theta = 0 \\ \rightarrow \gamma^2 - 2cos \theta \gamma + cos^2\theta + sin^2 \theta = 0 \\ \gamma^2 -2cos\theta\gamma + 1 = 0\)

여기서 2차방정식의 근의공식을 이용하자
근의공식 \(\rightarrow\) \(ax^2+bx+c=0\) 일 때,   \(x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\)
\(\therefore \gamma = \frac{2cos \theta \pm \sqrt{4cos^2\theta-4}}{2} \\ \rightarrow \gamma^2 = cos^2\theta \pm (cos^2 \theta-1)\)

잠깐 아래식 참고!
$sin^2\theta+cos^2\theta=1$를 이용하여 이렇게 변형해보자 $ \color{pink}{\Rightarrow} $ \(cos^2\theta-1=-sin^2\theta\)
\(\gamma^2 = cos^2\theta \pm -sin^2\theta \\ \gamma = cos\theta \pm isin\theta\)

오일러 공식으로 변환 가능하겠네
\(e^{\pm i\theta} = cos\theta \pm isin\theta\)
일단 오일러공식에 대한 자세한 설명은 고유벡터 구하고 진행하겠다

🧩회전행렬의 고유벡터 계산

case 1)   \(\gamma = cos\theta + isin\theta\)

\(Ax = \gamma x \\ \begin{bmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{bmatrix} \vec{x} = (cos\theta + isin\theta) \vec{x}\)
여기서 \(\gamma x\)를 \(\gamma I_2 x\)로 바꿔주자
\(\rightarrow\) \((cos\theta + isin\theta) \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} (cos\theta + isin\theta) & 0 \\ 0 & (cos\theta + isin\theta) \end{bmatrix}\)

그러면 \(Ax = \gamma I_2 x\)이 되는데, 여기서 우변을 좌변으로 넘기면?
\(\Rightarrow (A-\gamma I_2)x = 0 \\ \Rightarrow \begin{bmatrix} cos \theta-cos \theta-isin\theta & -sin \theta \\ sin \theta & cos \theta - cos \theta- isin\theta \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = 0 \\ \Rightarrow \begin{bmatrix} -isin\theta & -sin \theta \\ sin \theta & - isin\theta \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = 0\)

Ax=0 꼴이 되는데 여기서 연립방정식 풀면 아래처럼 고유벡터가 나온다
따라서   \(\vec{x} = \begin{bmatrix} i \\ 1 \end{bmatrix}\)

case 2)   \(\gamma = cos\theta - isin\theta\)

위와 똑같이 계산해주면 \(\vec{x} = \begin{bmatrix} -i \\ 1 \end{bmatrix}\)

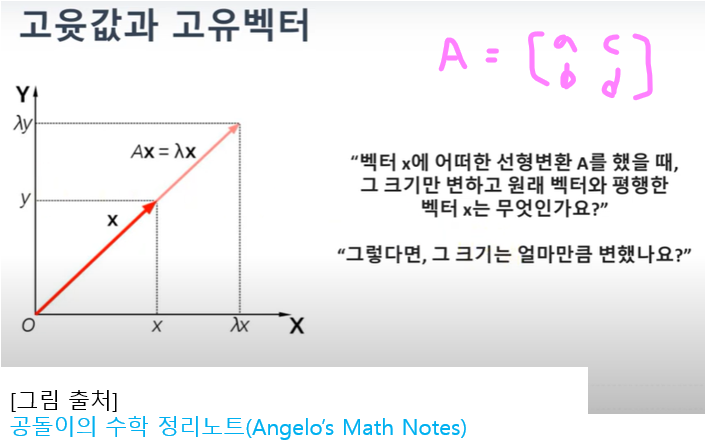
3. 복소수와 오일러공식

우선 복소수를 알기 위해서 실수부와 허수를 알아야 한다.
\(\color{pink}{\Rightarrow}\) \(x+iy\)
참 복소수 벡터 내적(길이)을 구하는 건 예를 들어 \(v = \begin{bmatrix} 1 \\ i \end{bmatrix}\)라고 할 때,
\(||v|| = \sqrt{v\cdot \bar v} = \sqrt{(1,i)\cdot(1,-i)} = \sqrt{1+1} \\ \therefore \sqrt2\)

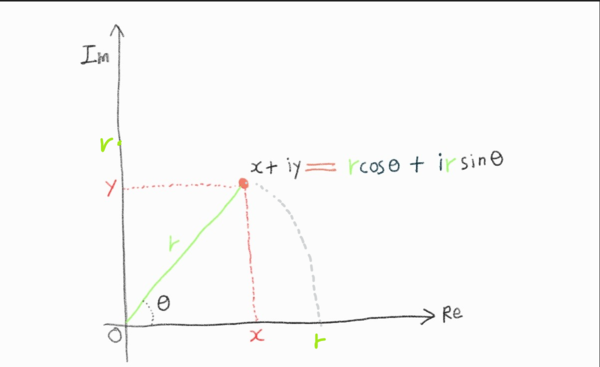
이제 \(x+iy\) 을 animation으로 나타내면 아래와 같다
위의 내용에서 \(x+iy\)와 \(\sqrt{(1,i)\cdot(1,i)}\)를 이해했다면, 아래 영상이 무슨 말인지 바로 이해할 것이다

1에서 i를 곱하면 90도 돌아서 i,
i에서 i 곱하면 90도 또 돌아서 -1
즉 스칼라배를 생각해보면 음수를 곱하는 것은 반대방향으로의 변환,
복소수를 곱하는 건 회전 을 의미한다.
혹시 지금도 무슨말인지 잘 몰라도 괜찮다.
밑의 시뮬레이션을 조작해보고 영상을 보면 100퍼 이해할 것이다

📐Euler’s Formula

\(e^{\pm i\theta} = rcos\theta \pm risin\theta\)

여기서 \(e^{i\theta}\)의 의미:
\(\color{pink}{\Rightarrow}\) r(반지름)이라는 숫자를 임의의 \(\theta\)라디안 만큼 회전시키겠다

진짜 완전 쉬운 이해 \(\Rightarrow sin90=1\),   \(cos90 = 0\)이니까,
오일러 공식을 참고하여 시뮬레이션을 돌릴 때 \(n\): 1~20 범위인데,
n이 커질수록 sin 값이 커지니까 1에 가까워진다
이제 오일러 공식에서 \(\theta\)가 커질 때의 관계가 눈에 보이지 않는가?

(혹시 n이 커지는거랑 1에 가까워지는게 무슨말인지 모르겠으면 아래 링크로 들어가자)

ʕ ·ᴥ·ʔ   반갑곰

4. 회전변환과 고유벡터의 상호작용

우선 한계점으로 복소 고유벡터는 시각화하는게 매우 어렵다.
복소수 자체가 이미 2차원의 수라서 그렇다
즉 $R^2$의 복소벡터는 실수 4개가 있어야 표현 가능하다   무슨말인지 RG?
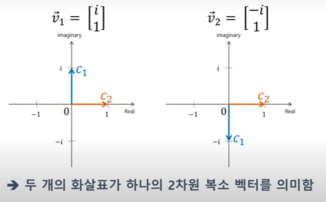
하지만 우리가 아까 위에서 얻은 고유벡터 2개인 \(\vec{v} = \begin{bmatrix} \pm i \\ 1 \end{bmatrix}\)로 2차원 복소벡터를 시각화 해보자!

$c_1$: 첫 번째 성분

$c_2$: 두 번째 성분

😎시각화

우선 반지름(r)을 1이라 하겠다 그러면 오일러공식은 아래와 같이 된다
\(e^{\pm i\theta} = cos\theta \pm isin\theta\)

• 여기서 고유벡터에 대한 선형변환은 딱 고윳값 만큼만 상수배한다
  
• 고윳값 $e^{i\theta}$와 $e^{-i\theta}$는 시계 or 반시계방향으로 $\theta$라디안 만큼의 회전을 의미한다
  (복소벡터, $\bar v_1$과 $\bar v_2$에 대해 고윳값 만큼 상수배
  $\Rightarrow$ 고유벡터를 시계 or 반시계로 $\theta$라디안 만큼 회전)
  

아래 시뮬레이션 2개를 조작하면서 우측 상단에 나오는 각도도 확인 가능하다

\(\gamma_1 = e^{i\theta}\)일 때 회전변환과 고유벡터의 상호 작용

\(\gamma_2 = e^{-i\theta}\)일 때 회전변환과 고유벡터의 상호 작용

참고

공돌이의 수학정리노트     회전 행렬의 고윳값, 고유벡터 (복소 고윳값, 고유벡터)의 의미